


Next: About this document ...
論理と集合要約 No.5
第5回目の主題 :

集合を扱う際は
個々の元を取り出し、
諸性質を論理で証明する。
例えば、
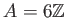 ,
,
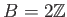 にたいして、
にたいして、
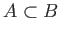 を示すには、
を示すには、
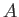 の各元
の各元 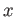 について、
について、
-
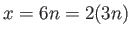 であることを示し、
であることを示し、
-
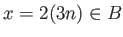 と結論する。
と結論する。
というステップを踏む。
同様に、
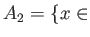
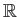
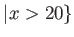 ,
,
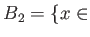
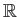
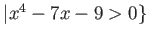 に対して、
に対して、
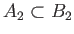 を示すには、
を示すには、
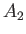 の各元
の各元 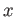 について、
について、
であることを示し、
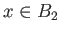 と結論する。
と結論する。
と良い。
問題 5.1
実係数の多項式
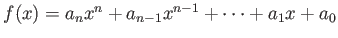
が、
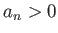
を満たすとする。
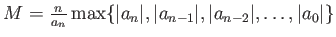
とおくと、
が成り立つことを示しなさい。
集合の一般論でも同様。
問題 5.2
集合
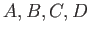
に対して、
を示しなさい。
問題 5.3
集合
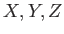
に対して、
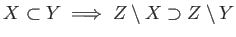
を示しなさい。
問題 5.4
集合族
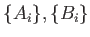
が与えられた時、包含関係
および
を示しなさい、
Yoshifumi Tsuchimoto
2016-05-16
![]()
![]() ,
,
![]() にたいして、
にたいして、
![]() を示すには、
を示すには、
![]()
![]()
![]() ,
,
![]()
![]()
![]() に対して、
に対して、
![]() を示すには、
を示すには、