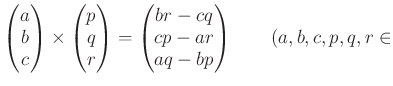Next: About this document ...
代数学演習 IB 問題 No.1

定義 1.1
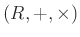
が環(正確には結合的環)であるとは、それが次の3つの条件を満たすときに言います。
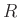 は
は 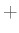 (加法) に関して加法群である。
その単位元(つまり、
(加法) に関して加法群である。
その単位元(つまり、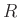 の加法に関する単位元)を 0
と書き、
の加法に関する単位元)を 0
と書き、
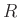 の零元と言います。
の零元と言います。
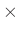 (乗法) は結合律を満たす。
(乗法) は結合律を満たす。
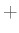 と
と  のあいだでは分配法則が成り立つ。すなわち、
のあいだでは分配法則が成り立つ。すなわち、
がすべての 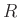 の元
の元 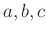 について成り立つ
について成り立つ
さらに
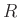
の元
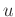
が
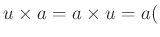
すべての $a&isin#in;R$ について
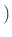
を満たすとき、
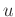
を
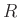
の単位元と言います。(普通は、単位元のことは
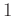
と書きます。)
簡単に言えば、普通の計算をやってると思って良いです。ただし、割り算ができないことと、積が可換とは限らないことが違います。また、乗法の 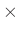 は省略することが多いです。例えば、
は省略することが多いです。例えば、
また、
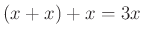 ,
,
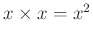 等と略記します。
等と略記します。
(演習の都合により、上の定義と今回(No.1)では、環の単位元の存在を仮定しません。
が、次回(No.2)からは、講義と歩調をあわせて、
環と言えば単位元をもつもののみを扱うことにします。)
定義 1.2
積が可換である環を可換環と言います。単位元が存在して、
0
でない元で割り算ができるような可換環を体と言います。
問題 1.1 (各1)
.
環
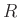
の元
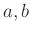
に対して、(1):
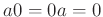
, (2):
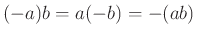
,
(3):
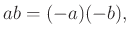
(4):
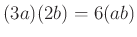
が成り立つことを、
環の定義のどの部分を用いているかに
十分注意しながら示しなさい。
(
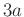
は
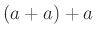
の略記であって、
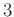
と
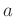
のかけ算では
ないことに注意。)
問題 1.2 (全部で1.)
環の零元と単位元は存在したとしてもただひとつであることを示しなさい。
(ヒント1:
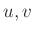
を二つの零元とすると
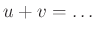
)
(ヒント2:
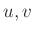
を二つの単位元とすると
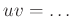
)
問題 1.4
集合
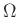
をひとつ取る。このとき、
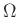
の部分集合の全体
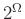
は対称差
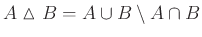
を「和」に、
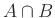
を「積」として採用することで環になる(!)。このことを(一部ではあるが)
確かめるために、次のことを示せ。ただし必要な集合算の定理
(論理と集合の教科書のはじめの方にのっているような比較的安易なもの)
は証明せずに適宜引用して使ってよい。
- 「和」(対称差)は結合律を満たすことを証明せよ。
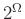 の「和」(対称差)に関する単位元はなにか、
理由をつけて答えなさい。
の「和」(対称差)に関する単位元はなにか、
理由をつけて答えなさい。
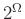 の 「積」に関する単位元はなにか。理由をつけて答えなさい。
の 「積」に関する単位元はなにか。理由をつけて答えなさい。
問題 1.6 (全部で1)
次の各集合は指定した演算で環ではないことを示しなさい。
(和は通常のものを選ぶ。)
-
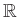
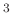 に積として外積、つまり
に積として外積、つまり
により定まる二項演算を入れたもの。
- 実数を成分とした二次正方行列の全体
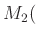
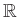
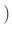 に、積として交換子積
に、積として交換子積
を入れたもの。ただし右辺に現れる演算は行列の普通の演算である。
問題 1.8 (各1)
整数全体の集合
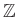
に「新しい和」

を
で定義したとき
- この新しい和は可換であることを示しなさい。
- この新しい和は結合律をみたすこと、すなわち
がなりたつことを示しなさい。
- この新しい和に関して単位元は存在するだろうか?
- この新しい和に関して各
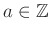 の逆元は存在するだろうか?
の逆元は存在するだろうか?
問題 1.9 (各1)
整数全体の集合
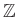
に「新しい積」
を
で定義したとき
- この新しい積は可換であることを示しなさい。
- この新しい積は結合律をみたすこと、すなわち
がなりたつことを示しなさい。
- この新しい積に関して単位元は存在するだろうか?
- この新しい積に関して各
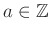 の逆元は存在するだろうか?
の逆元は存在するだろうか?
-
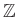 に加法として前問の
に加法として前問の  , 乗法として本問の
, 乗法として本問の  を
導入したものは環であるといえるだろうか?
を
導入したものは環であるといえるだろうか?



Next: About this document ...
2016-10-14
![]()