微分積分学基礎 No.1要約

今日のテーマ:実数

関数の概念：

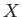
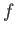
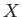
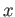
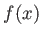
定義 1.1   集合 $X$ 上の実数値関数$f$ とは、 $X$ の各元 $x$ に対して、その値 $f(x)$ が (誰がやっても正しくやる限りはただひとつ)定まっている時に いう。

「ある時刻での気圧」は平面の領域上の関数とみなせる。

→多変数関数や関数列を扱う必要が生じるがまずは 数列や、一変数関数を扱うのが基本になる。

定義 1.2   以下この講義では次のような記号を用いる。

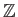1. ${\mbox{${\mathbb{Z}}$}}$ : 整数全体のなす集合。

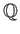2. $\mbox{${\mathbb{Q}}$}$ : 有理数全体のなす集合。

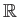3. $\mbox{${\mathbb{R}}$}$ : 実数全体のなす集合。

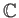4. ${\mathbb{C}}$ : 複素数全体のなす集合。

◎集合と、その元との区別が大事。 「実数の集合を一つ考える。」というのと、「実数を一つ考える。」というのを よく意識して区別すること。

定理 1.3   次の不等式が成り立つ。

1. $x\in$   $\mbox{${\mathbb{R}}$}$ に対して、 $-\vert x\vert \leq x \leq \vert x\vert$ .
2. (三角不等式) $x,y\in$   $\mbox{${\mathbb{R}}$}$ に対して、 $\vert x+y\vert \leq \vert x\vert+\vert y\vert.$

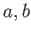
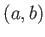
定義 1.4   実数 $a,b$ について、閉区間 $[a,b]$ と開区間 $(a,b)$ を つぎの式で定める。

$$[a,b] =\{x \in \mbox{${\mathbb{R}}$} \vert a\leq x \leq b\}$$

$$(a,b) =\{x \in \mbox{${\mathbb{R}}$} \vert a < x < b\}$$

以下、この講義では、 整数、有理数、実数の、和、差、積、商、等号、不等号。を 自由に用いる。 その他、実数の完備性というのも用いるのであるが、それについては次回。