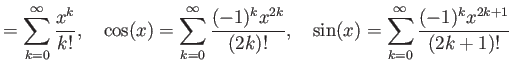Next: About this document ...
微分積分学基礎 No.8要約
今日のテーマ:高階微分,テイラー展開
定義 8.1
一変数関数
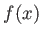
の導関数
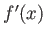
を考える。
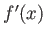
が
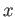
の関数として微分可能であるとき、
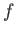
は2回微分可能であると言う。
さらにこのとき
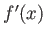
の導関数を
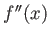
もしくは
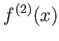
と書き、
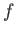
の
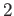
次(
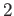
階) の導関数とよぶ。
同様にして、
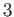
次の導関数

,
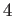
次の導関数
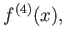
...
が定義される。
定義 8.2
開区間
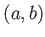
で定義される関数
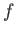
が
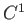
級であるとは、
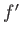
が定義されてそれが連続であるときにいう。同様に、
正の整数
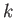
に対して、
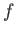
が
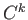
級であるとは、
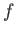
が
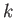
回微分可能で、なおかつ
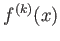
が連続であるときにいう。
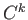
級関数のことを
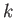
階(回)連続微分可能な
関数と呼ぶこともある。
任意の
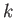
に対して
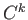
級であるような関数のことを
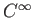
級関数とか、
無限回微分可能な関数とよぶ。
前回、次のことをロピタルの定理を何度も使うことにより証明した。
定理 8.3 (漸近展開)
一変数関数
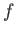
が
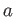
の近くで
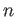
回微分可能であれば、
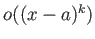 のところ(剰余項)は平均値の定理によって少しは具体的に記述できる。
のところ(剰余項)は平均値の定理によって少しは具体的に記述できる。
*以下少し難しいが、面白いので付け加えておく。
この講義では後に(定積分について議論したあとで)次の形で証明することにする。
定理 8.4 (テイラー展開(積分による剰余項の表記))
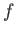
が
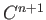
級の時
剰余項が比較的小さく、
テイラ-展開の(剰余項を除いた部分の)
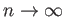 の極限が元の関数に
近づく場合がある。そのような関数を実解析関数と呼ぶ。
の極限が元の関数に
近づく場合がある。そのような関数を実解析関数と呼ぶ。
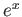 ,
, 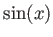 ,
, 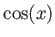 は実解析関数の例である。
これらの関数は、テイラー展開(の
は実解析関数の例である。
これらの関数は、テイラー展開(の 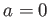 のバージョン(マクローリン展開と呼ぶ)
で定義してしまうことも可能である。
のバージョン(マクローリン展開と呼ぶ)
で定義してしまうことも可能である。
さらに、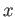 の取りうる値を実数のみから複素数まで広げて、これらの関数を
拡張できる。とくに:
の取りうる値を実数のみから複素数まで広げて、これらの関数を
拡張できる。とくに:
これによって三角関数の加法定理を指数関数の法則から導いたりできる。
2017-06-01
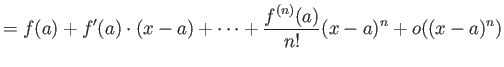
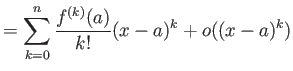
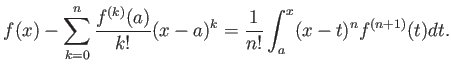
![]() の極限が元の関数に
近づく場合がある。そのような関数を実解析関数と呼ぶ。
の極限が元の関数に
近づく場合がある。そのような関数を実解析関数と呼ぶ。
![]() ,
, ![]() ,
, ![]() は実解析関数の例である。
これらの関数は、テイラー展開(の
は実解析関数の例である。
これらの関数は、テイラー展開(の ![]() のバージョン(マクローリン展開と呼ぶ)
で定義してしまうことも可能である。
のバージョン(マクローリン展開と呼ぶ)
で定義してしまうことも可能である。