![]() 行列の演算と実数の演算。
行列の演算と実数の演算。
行列の和、差、積は実数を扱うのと同様の扱いで良いのだが、
◎ 特別な行列
すべての成分が 0
の行列を零行列とかゼロ行列といい、
サイズが ![]() のゼロ行列を
のゼロ行列を ![]() で表す。
で表す。
行と列の数が等しい行列を正方行列という。
正方行列の
![]() で、
で、![]() であるような成分
であるような成分
![]() を
を ![]() の対角成分という。対角成分がすべて
の対角成分という。対角成分がすべて ![]() で、残りの成分が 0
であるような
正方行列のことを、単位行列と言い、サイズが
で、残りの成分が 0
であるような
正方行列のことを、単位行列と言い、サイズが ![]() の単位行列を
の単位行列を ![]() とか、
とか、
![]() と表記する。
と表記する。
◎ クロネッカーのデルタ。
クロネッカーのデルタと呼ばれる記号
![]() を
を
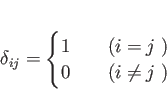
で定める。単位行列はクロネッカーのデルタを成分にもつ行列である。
がなりたつ。
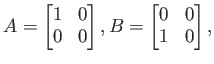
とおくと、
● http://www.math.kochi-u.ac.jp/docky/kogi にこのプリント
を提供する.