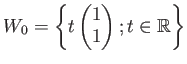 も、「同じ形」をしている。
このような2つを同時に扱うのには、成分を見るのではなく、
和と、スカラー倍という道具のみを用いて記述することが
大事になる。例えば、成分がすべて 0
のベクトル (0
ベクトル) は
も、「同じ形」をしている。
このような2つを同時に扱うのには、成分を見るのではなく、
和と、スカラー倍という道具のみを用いて記述することが
大事になる。例えば、成分がすべて 0
のベクトル (0
ベクトル) は
今日のテーマ: ベクトル
実数直線も、
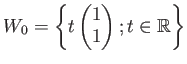 も、「同じ形」をしている。
このような2つを同時に扱うのには、成分を見るのではなく、
和と、スカラー倍という道具のみを用いて記述することが
大事になる。例えば、成分がすべて 0
のベクトル (0
ベクトル) は
も、「同じ形」をしている。
このような2つを同時に扱うのには、成分を見るのではなく、
和と、スカラー倍という道具のみを用いて記述することが
大事になる。例えば、成分がすべて 0
のベクトル (0
ベクトル) は
![]() の解と見ることもできる。
の解と見ることもできる。
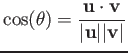 なる
なる