


Next: About this document ...
理工系線形代数学 No.12要約
今日のテーマ: 線形写像、線形変換
ベクトル空間 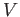 から ベクトル空間
から ベクトル空間 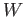 への写像で、
和を和に、スカラー倍をスカラー倍に写すものを線形写像という。
ベクトル空間
への写像で、
和を和に、スカラー倍をスカラー倍に写すものを線形写像という。
ベクトル空間 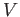 からそれ自身への線形写像を線形変換という。
からそれ自身への線形写像を線形変換という。
命題 12.1
ベクトル空間 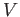 ,
, 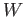 の基底をとると、
の基底をとると、
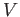 から
から 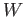 への線形写像は行列で書くことができる。
への線形写像は行列で書くことができる。
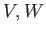 の次元をそれぞれ
の次元をそれぞれ 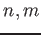 とすると、その行列は
とすると、その行列は
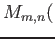
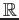
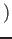 の元である。とくに、
の元である。とくに、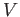 から
から 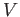 への線形変換
は
への線形変換
は
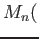
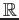
 の元で表現できる。
の元で表現できる。
定義 12.2
線形写像
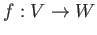
に対して、その核

と
像
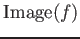
を
で定義する。
行列の行基本操作を使うことにより、次のことがわかる。
命題 12.3 (次元定理)
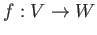 が有限次元ベクトル空間の間の線形写像なら、
が有限次元ベクトル空間の間の線形写像なら、
この量は
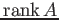 と等しい。
と等しい。
線形変換では、「変換後と変換前を比べる」ことができる。
とくに、対角行列による変換は考えやすい。
定義 12.4
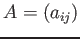
が対角行列であるとは、対角成分以外の
成分が 0
, すなわち
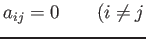
のとき
が成り立つときにいう。
スペースの都合で、この「要約」では「対角行列
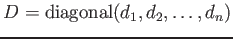 」
という書き方をする。対角成分が
」
という書き方をする。対角成分が
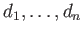 であとは 0
であるような
行列という意味である。
であとは 0
であるような
行列という意味である。
対角行列同士の和や積は特別に易しい。
これは、対角行列
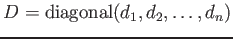 に対しては、基本ベクトル
に対しては、基本ベクトル
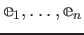 が
が
を満たしているからである。
命題 12.5
対角行列

 に対して、
に対して、
-
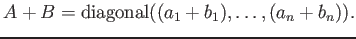
-
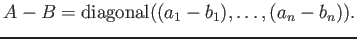
-

-

つまり、対角行列の線形結合、積は成分ごとに行って良い。
2017-07-26
![]() から ベクトル空間
から ベクトル空間 ![]() への写像で、
和を和に、スカラー倍をスカラー倍に写すものを線形写像という。
ベクトル空間
への写像で、
和を和に、スカラー倍をスカラー倍に写すものを線形写像という。
ベクトル空間 ![]() からそれ自身への線形写像を線形変換という。
からそれ自身への線形写像を線形変換という。
![]() に対しては、基本ベクトル
に対しては、基本ベクトル
![]() が
が