PROOF..
(1) Assume
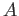
is a local ring with the maximal ideal
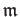
.
Then for any element
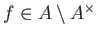
,
an ideal
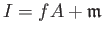
is an ideal of
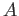
.
By Zorn's lemma, we know that
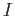
is contained in a maximal ideal of
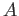
.
From the assumption, the maximal ideal should be
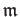
.
Therefore, we have
which shows that
The converse inclusion being obvious (why?), we have
(2) The ``only if'' part is an easy corollary of (1).
The ``if'' part is also easy.
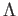
DEFINITION 05.13
Let
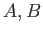
be local rings
with maximal ideals

respectively.
A local homomorphism
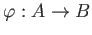
is a homomorphism which
preserves maximal ideals. That means, a homomorphism
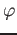
is said to be local
if
![]()