DEFINITION 07.4
An
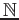
-graded ring
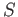
is a commutative ring with a direct sum decomposition
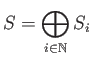
(as a module)
such that
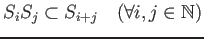
holds.
We define its irrelevant ideal
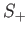
as
An element
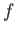
of
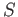
is said to be homogenous if it is an element of
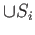
. An ideal of
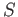
is said to be homogeneous if it is generated
by homogeneous elements. Homogeneous subalgebras are defined in a same way.
DEFINITION 07.5
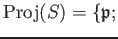
$
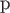
$ is a homogeneous prime ideal of $S$
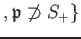
For any homogeneous element
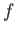
of
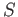
, we define a subset
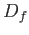
of

as
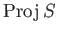
has a topology (Zariski topology) which is defined by
employing
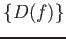
as an open base.
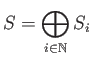 (as a module)
(as a module)
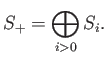
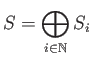 (as a module)
(as a module)
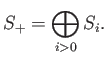
![$\displaystyle D_f \sim \operatorname{Spec}(S[\frac{1}{f}])_0).
$](img42.png)