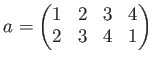
今日のテーマ: 置換群 ・ 整数の加法群
置換
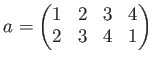
は、
というようにも書く。
二つの置換の結合(演算)は通常《後ろから読》む。たとえば、
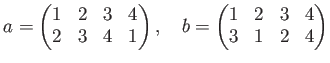
の掛け算
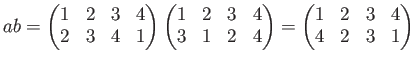
つまり、例えば
いくつかの元
![]() を順繰りに変える置換、すなわち
を順繰りに変える置換、すなわち
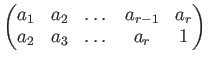
のことを 巡回置換と呼び、
任意の置換は互いに同じ文字を含まない巡回置換の積として表すことができる。例えば 、置換
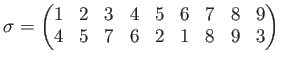
をよくみてみると、次のような変身の様子が分かる。
したがって、
であることが分かる。
置換の概念および記号は、
![]() のような集合だけではなく、
他の集合でも使える。
のような集合だけではなく、
他の集合でも使える。
たとえば、
![]() の元を一斉に
の元を一斉に
![]() 倍することは
倍することは
なる置換に対応する。
![]() は可換群なのであった。
演算としては加法
は可換群なのであった。
演算としては加法 ![]() を用いる。
を用いる。
![]() に対してももちろん群の一般論が使える。
ただし、記法に関しては注意が必要である。
に対してももちろん群の一般論が使える。
ただし、記法に関しては注意が必要である。
![]() の部分集合
の部分集合
![]() を考えよう。話を見えやすくするために
を考えよう。話を見えやすくするために ![]() とし、
とし、
![]() を考える。
群の一般論により、剰余集合
を考える。
群の一般論により、剰余集合
![]() が存在する。
それは、
が存在する。
それは、
により整数を類別したものである。
![]() を法とした剰余類というのを高校で習った人もいるかもしれない。
それらの人にとっては、
を法とした剰余類というのを高校で習った人もいるかもしれない。
それらの人にとっては、
![]() というのは
というのは
![]() と同義である。
と同義である。
![]() と
と
![]() の間に
の間に
という一対一対応があることにも注意しておこう。