![]()
準同型定理の適用例
![]() から
から
![]() への写像
への写像 ![]() を
を
で定義すると、
が
![]() から
から
![]() への写像
への写像 ![]() を
を
で定義すると、
が
により定まる。
ベクトル空間 ![]() から
から ![]() への線形写像
への線形写像 ![]() は、
は、![]() から
から ![]() への
群準同型である。従って、群の準同型定理が適用できて、
(加法)群の同型
への
群準同型である。従って、群の準同型定理が適用できて、
(加法)群の同型
![]() が成り立つことがわかる。じつはこの同型写像は線形空間の準同型定理で
言及されているものと写像としては同じである。
(線形写像のほうがスカラー倍も考えている分だけ情報が多い。)
が成り立つことがわかる。じつはこの同型写像は線形空間の準同型定理で
言及されているものと写像としては同じである。
(線形写像のほうがスカラー倍も考えている分だけ情報が多い。)
問題
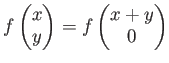
で定義するとき、