Next: About this document ...
今日のテーマ:分離拡大
以下、代数拡大体の性質を見ることが話題の中心になる。
既存の体 ![]() にたいして、
その上の代数的な元
にたいして、
その上の代数的な元 ![]() を付け加えて新しい体
を付け加えて新しい体 ![]() を
つくることができるのであった.
それは
を
つくることができるのであった.
それは ![]() の
の ![]() 上の最小多項式
上の最小多項式 ![]() を用いて作られる
を用いて作られる
一般に、与えられた多項式 ![]() に対して、
に対して、![]() の根を次々に
の根を次々に ![]() に加えることにより、
に加えることにより、
![]() の分解体を作ることができ、なかんづく最小分解体は
の分解体を作ることができ、なかんづく最小分解体は
![]() によって同型を除いて一意に決まるのであった。
によって同型を除いて一意に決まるのであった。
分離性は代数学を進んで学びたい者にとっては大事な概念であるが、
その重要性や取り扱い方は一旦ガロア理論に習熟してからのほうが
よく分かるように思える。したがってこの講義では
定義と、「標数 0 のとき」についての注意をしておくに止めよう。
(体 ![]() において、
において、![]() を何回か足すと 0 になる場合がある。
そのような「回数」を
を何回か足すと 0 になる場合がある。
そのような「回数」を ![]() の標数とよぶ。もっとカッコヨク言えば
次のようになる。)
の標数とよぶ。もっとカッコヨク言えば
次のようになる。)
例えば素数 ![]() を与えたとき、
を与えたとき、
![]() は 標数
は 標数 ![]() である。
である。
![$\displaystyle \frac{d}{d X} : K[X] \to K[X]
$](img15.png)
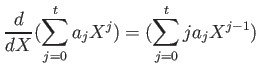
上の命題により、
![]() ならば
ならば ![]() の代数拡大体は必ず
の代数拡大体は必ず ![]() 上
分離的である
上
分離的である
分離性を意識するといろいろな話がラクにすすむ。例えば: