代数学III要約 No.13
ガロア対応の例
例 13.1
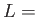
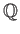
![% latex2html id marker 1075
$ (\sqrt[3]{11}, \omega), \quad K=$](img3.png)
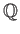
.
(但し
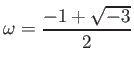
).
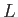
は
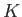
のガロア拡大である。
ガロア群
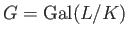
の生成元としては
で定義される
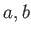
がとれて、
を満たす。ゆえに、
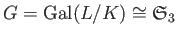
(3次の対称群)
の部分群は
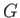
と
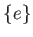
のほかに:
- 位数
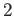 のもの 3つ。(
のもの 3つ。(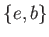 ,
, 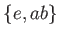 ,
,
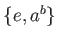 ).
).
- 位数
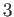 のもの 1つ (
のもの 1つ (
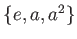 )。
)。
それらに対応する中間体は
例 13.2
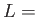
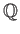
![% latex2html id marker 1130
$ (\sqrt[4]{3}, i), \quad K=$](img25.png)
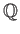
. (但し
.)
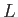
は
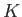
のガロア拡大である。
ガロア群
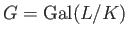
の生成元としては
で定義される
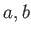
がとれて、
を満たす。ゆえに、
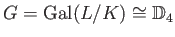
(二面体群)
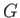
の部分群は
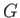
と
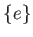
のほかに:
それらに対応する中間体は
問題 13.1
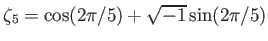
とおく(
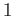
の
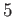
乗根)。
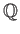
![% latex2html id marker 1211
$ (\sqrt[5]{2},\zeta_5)$](img48.png)
と
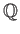
のあいだの中間体で、
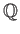
上拡大次数が
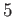
のものを
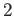
つ以上求めよ。
◎ 二重根号
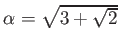 とおく。このとき、
とおく。このとき、
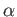 の
の
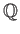 上の最小多項式は
上の最小多項式は
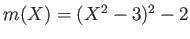 である。
である。
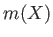 の最小分解体
の最小分解体 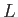 は
は
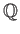
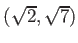 を部分体として含む。
を部分体として含む。
- ガロア群
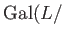
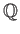
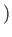 の元
の元 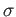 で、
で、
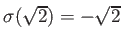 ,
,
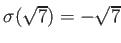 を満たすものが存在する。
を満たすものが存在する。
-
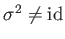 .
.
-
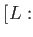
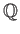
![$ ]=8$](img61.png) で、
で、
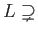
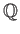
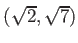 .
.
-
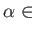
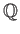
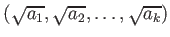 を満たすような
を満たすような
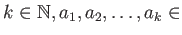
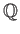 は存在しない。
は存在しない。
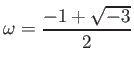 ).
).
![\begin{displaymath}
% latex2html id marker 1086a:
\begin{cases}
\sqrt[3]{11}&\...
...}&\mapsto \sqrt[3]{11} \\
\omega&\mapsto \omega^2
\end{cases}\end{displaymath}](img8.png)
![\begin{displaymath}
% latex2html id marker 1141a:
\begin{cases}
\sqrt[4]{3}&\m...
...}
\sqrt[4]{3}&\mapsto \sqrt[4]{3} \\
i &\mapsto -i
\end{cases}\end{displaymath}](img27.png)
![]() とおく。このとき、
とおく。このとき、