微分積分学基礎 No.3要約
今日のテーマ:(実数区間上の)連続関数
命題 3.2
区間
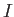
上で関数
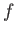
が定義され、
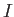
の各点
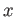
について
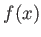
が区間
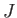
に属するとする。
このとき、
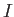
上の関数(
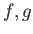
の合成関数)
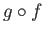
が
で定義される。さらに、
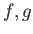
が連続なら
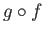
も連続である。
定理 3.3
塀区間
![$ I=[a,b]$](img15.png)
上の連続関数
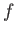
が狭義単調増加であるとする。
すなわち、
と仮定する。このとき、
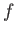
の逆関数
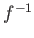
が定義されて、
連続である。
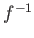
は
![$ J=[f(a),f(b)]$](img18.png)
上定義される関数であって、
任意の
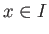
に対し、
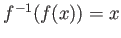
を満たし、
また
任意の
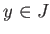
に対し、
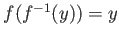
を満たす。
参考:
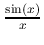 の値の表
の値の表
| x |
0 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
... |
|
|
|
|
|
| sin(x) |
0 |
0.0998 |
0.1987 |
0.2955 |
0.3894 |
0.4794 |
... |
|
|
|
|
|
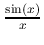 |
* |
0.998 |
0.993 |
0.985 |
0.974 |
0.959 |
... |
|
|
|
|
|
![]() の値の表
の値の表