Next: The ring of -adic Up: , , and the Previous: Idempotents
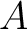 be a commutative ring.
For any
be a commutative ring.
For any 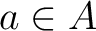 , we denote by
, we denote by ![$[a]$](img22.png) the element of
the element of
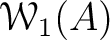 defined as follows:
defined as follows:
![$\displaystyle [a]=(1-a T)_W
$](img23.png)
![$[a]$](img22.png) the “Teichmüller lift” of
the “Teichmüller lift” of 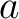 .
.
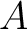 be a commutative ring. Then:
be a commutative ring. Then:
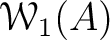 is a commutative ring
with the zero element
is a commutative ring
with the zero element ![$[0]$](img25.png) and the unity
and the unity ![$[1]$](img26.png) .
.
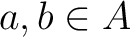 , we have
, we have
![$\displaystyle [a]\cdot [b]=[a b]
$](img28.png)
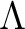
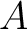 be a commutative ring.
If
be a commutative ring.
If 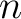 is a positive integer which is invertible in
is a positive integer which is invertible in 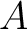 ,
then
,
then
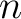 is invertible in
is invertible in
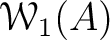 . To be more precise, we have
. To be more precise, we have
![$\displaystyle \frac{1}{n}\cdot [1]= \left( (1-T)^{\frac{1}{n}}\right)_W
= \left((1+\sum_{j=1}^\infty \binom{\frac{1}{n}}{j} (-T)^j \right)_W.
$](img30.png)
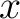 of
of ![$A[[T]]$](img32.png) such that
such that
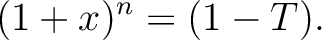
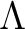
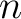 be a positive integer. Let
be a positive integer. Let 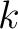 be a non negative integer.
Then we have always
be a non negative integer.
Then we have always
![$\displaystyle \binom{\frac{1}{n}}{k}\in \mathbb{Z}\left[\frac{1}{n}\right].
$](img35.png)
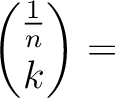 |
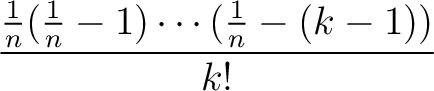 | |
 |
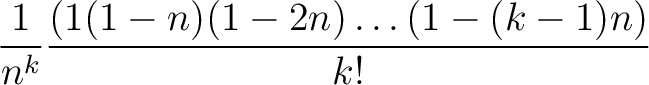 |
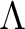
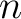 be a positive integer. Let
be a positive integer. Let 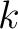 be a non negative integer.
Let
be a non negative integer.
Let
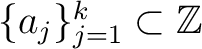 be an arithmetic progression of common difference
be an arithmetic progression of common difference 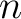 .
Then:
.
Then:
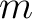 which is relatively prime to
which is relatively prime to 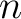 , we have
, we have
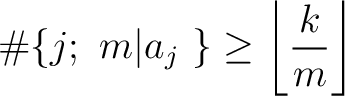
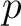 which does not divide
which does not divide 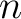 , let us define
, let us define
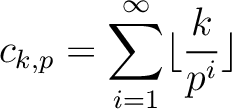
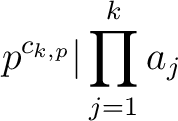

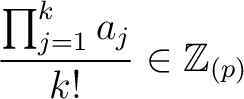
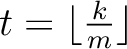 .
Then we divide the set of first
.
Then we divide the set of first 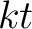 -terms
of the sequence
-terms
of the sequence 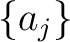 into disjoint sets in the following way.
into disjoint sets in the following way.
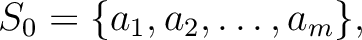 | ||
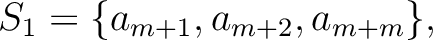 | ||
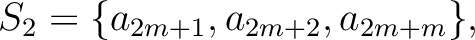 | ||
 | ||
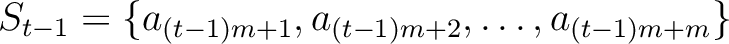 |
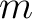 is coprime to
is coprime to 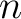 , we see that
each of the
, we see that
each of the 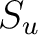 gives a complete representative of
gives a complete representative of
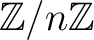 .
.
(2): Apply (1) to the cases where
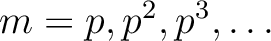 and count the
powers of
and count the
powers of 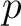 which appear in
which appear in 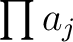 .
.
(3): Easy.
(4) is a direct consequence of (2),(3).
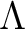
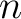 which is invertible in a commutative ring
which is invertible in a commutative ring 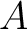 ,
we define an element
,
we define an element 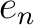 as follows:
as follows:
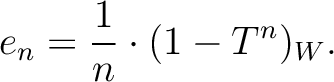
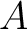 be a commutative ring. Then for any positive
integer
be a commutative ring. Then for any positive
integer 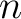 which is invertible in
which is invertible in 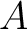 , we have:
, we have:
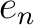 is an idempotent.
is an idempotent.
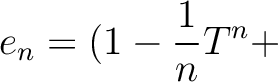 (higher order terms)
(higher order terms)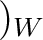
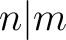 , with
, with 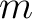 invertible in
invertible in 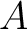 ,
then
,
then
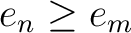 in the order of idempotents.
in the order of idempotents.
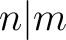 , then we have
, then we have
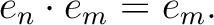
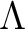
It should be important to note that the range of the projection 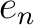 is easy to describe.
is easy to describe.
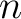 be an integer which is invertible in
be an integer which is invertible in 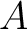 .
Then the range
.
Then the range
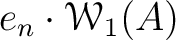 of the projection
of the projection 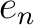 is equal to
is equal to
![$\{
(f)_W \vert f \in 1+ T^n A[[T^n]]
\}
$](img70.png) . It is isomorphic to
. It is isomorphic to
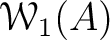 .
.
ARRAY(0x55f8edf09890)