DEFINITION 20.2
For any commutative ring
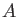
, let us define

to be the submodule of
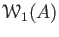
generated by
all the images
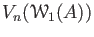
, where
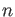
is a positive
integer which is not divisible by
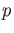
:
Let us denote by
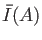
its closure. Then we define:
PROOF..
Surjectivity: Every element
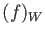
of
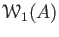
may be
written as
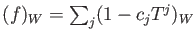
.
Knowing that
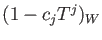
is an element of

whenever
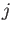
is not
divisible by
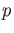
, we see that
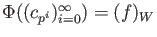
.
Injectivity:
Assume
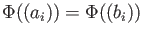 . Let
. Let 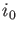 be the smallest integer
be the smallest integer 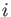 such that
such that
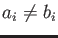 . Then by subtraction we obtain an equation
. Then by subtraction we obtain an equation
in
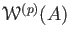
.
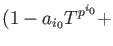
higher order terms
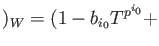
higher order terms
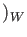
Since we know that the terms of order
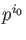
are not affected by
additions of elements of
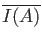
,
we see
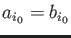
, which is a contradiction.
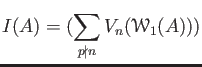
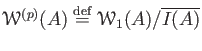
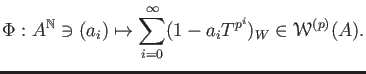
![]() . Let
. Let ![]() be the smallest integer
be the smallest integer ![]() such that
such that
![]() . Then by subtraction we obtain an equation
. Then by subtraction we obtain an equation
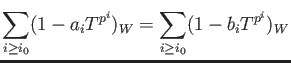
![]()