Next: About this document ...
注意:
「部分環」の定義により、
![]() は(
は(![]() が何であっても)
常に
が何であっても)
常に ![]() の単位元
の単位元 ![]() を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから
を元としてもつ。
しかし、単位元の存在を意識しておくために、以下では
始めから ![]() には
には ![]() の単位元
の単位元 ![]() が入ったものだけを考えることにする。
が入ったものだけを考えることにする。
上の補題の証明の途中で、次の補題が必要になるので、ここに掲げておく。
実際には、生成される部分環には次のパターンのものがよく使われる。
この記法によれば、上の例の (4),(5) はそれぞれ次のように書ける。
このように、
![]() が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
が実際にはどのような元を
もつのか決定することも基本的で、重要である。それは通常
次の手順で行う。
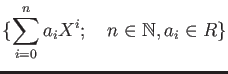
![% latex2html id marker 1343
$\displaystyle \{\sum_{i=0}^n a_iX^i ;\quad n\in \mathbb{N}, a_i \in R\}
=\langle R\cup \{X\} \rangle_{\text{ring}}=R[X]
$](img29.png)
注意
本講義 の範囲では他に
![]()
![]()
![]() 等が重要になる。
(
等が重要になる。
(
![]() ,
,
![]() ,
,
![]() は全て体である。すなわち積は可換であり、
0 以外の各元は逆元を持つ。)
は全て体である。すなわち積は可換であり、
0 以外の各元は逆元を持つ。)
同様にして、2変数多項式環 ![]() ,3変数多項式環
,3変数多項式環 ![]() 等が定義される。
等が定義される。
![% latex2html id marker 1364
$\displaystyle R[X,Y]=\{\sum_{\substack{i,j\geq 0\\ \text{(有限和)}}}
a_{i,j} X^i Y^j ; a_{i,j}\in R\}
$](img36.png)
![% latex2html id marker 1366
$\displaystyle R[X,Y,Z]=\{\sum_
{\substack{i,j,k\geq 0\\ \text{(有限和)}}}
a_{i,j} X^i Y^j Z^k ; a_{i,j,k}\in R\}
$](img37.png)
![% latex2html id marker 1372
$\displaystyle R[X_1,X_2,\dots, X_n]
=\{
\sum_
{
{...
...^{i_1}
X_2^{i_2}
X_3^{i_3}
\dots
X_n^{i_n}
;a_{i_1,i_2,\dots, i_n}\in R \}
$](img39.png)
多項式
![]() は書くのが面倒なので、多重指数を用いると便利である。
は書くのが面倒なので、多重指数を用いると便利である。
![]() という略記法を用いると、
という略記法を用いると、![]() は
は
![]() と簡略化して書ける。
定義により、
環
と簡略化して書ける。
定義により、
環
![]() は
環
は
環
![]() 上の
上の ![]() を変数とする
一変数多項式環と同じものとみなせる。
を変数とする
一変数多項式環と同じものとみなせる。