Next: About this document ...
今日のテーマ: 直交射影を表す行列
まずは復習から:
計量ベクトル空間 ![]() において、
において、
![]() が計量ベクトル空間、
が計量ベクトル空間、![]() が有限次ベクトル空間のとき、
が有限次ベクトル空間のとき、
![]() を
を ![]() の正規直交基底に採ると、
の正規直交基底に採ると、
![]() は
は ![]() の元であって、
の元であって、
![]() は
は![]() の元、
の元、
![]() と分解できるのであった。
と分解できるのであった。![]() は
は ![]() への直交射影と呼ばれる。
への直交射影と呼ばれる。
以下では、標準的な内積を用いる。
正方行列 ![]() に対して、
に対して、 ![]() の列ベクトルが正規直交系をなすとき、
の列ベクトルが正規直交系をなすとき、
![]() を直交行列と呼ぶ。
を直交行列と呼ぶ。
前回までの「やってみよう問題」から:
ある計量ベクトル空間 ![]() のベクトル
のベクトル
![]() が、
が、
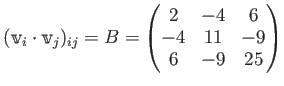
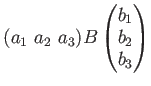
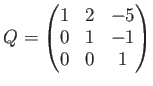 とおくと、
とおくと、
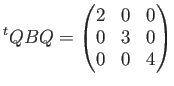
前回までのやってみよう問題では、上の ![]() の代わりに
の代わりに
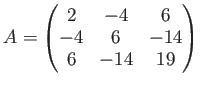
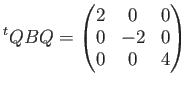
(ただし、本講義の本題からははずれますが、 このような「長さの二乗にあたるものが 負であるようなベクトルを考えに入れる必要のある系 (不定計量のベクトル空間)」も現代では相対論を始め色々なところで 出てくる興味深いものではあります。)