Next: Bibliography
Yoshifumi Tsuchimoto
For any projecvite variety
We quote the famous
![]()
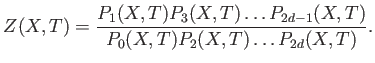
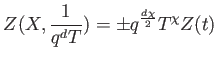
It is a profound theorem, relating the number of rational points
![]() of
of ![]() over finite fields
and the topology of
over finite fields
and the topology of
![]() .
.
For a further study we recommend [1, Appendix C],[2], [3].