Next: About this document ...
Yoshifumi Tsuchimoto
Let us site wikipedia:
(https://en.wikipedia.org/wiki/Lefschetz_fixed-point_theorem with some
modifications by Tsuchimoto-consult the original page for details)
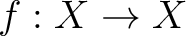
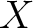 to itself.
Define the Lefschetz number
to itself.
Define the Lefschetz number 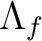 of
of 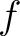 by
by
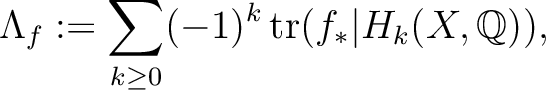
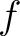 on
on
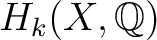 ,
the singular homology groups of
,
the singular homology groups of 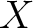 with rational coefficients.
A simple version of the Lefschetz fixed-point theorem states: if
with rational coefficients.
A simple version of the Lefschetz fixed-point theorem states: if
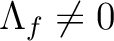 ,
then
,
then 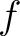 has at least one fixed point, i.e.,
there exists at least one
has at least one fixed point, i.e.,
there exists at least one 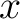 in
in 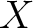 such that
such that 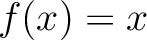 .
In fact, since the Lefschetz number has been defined at the homology level, the conclusion can be extended to say that any map homotopic to
.
In fact, since the Lefschetz number has been defined at the homology level, the conclusion can be extended to say that any map homotopic to 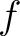 has a fixed point as well.
has a fixed point as well.
A stronger form of the theorem, also known as the Lefschetz-Hopf theorem,
states that, if 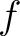 has only finitely many fixed points, then
has only finitely many fixed points, then
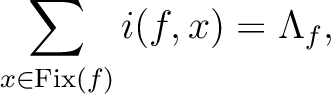
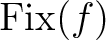 is the set of fixed points of
is the set of fixed points of 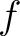 ,
and
,
and 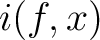 denotes the index of the fixed point
denotes the index of the fixed point 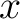 .
From this theorem one deduces the Poincaré-Hopf theorem for vector fields
.
From this theorem one deduces the Poincaré-Hopf theorem for vector fields