Next: About this document ...
今日のテーマ:

体 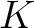 上の一変数既約多項式
上の一変数既約多項式 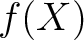 が与えられているとする。
が与えられているとする。
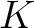 に
に  の根
の根 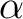 を付け加えてできたような体
を付け加えてできたような体
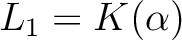 を
つくることができるのであった。
もちろん、
を
つくることができるのであった。
もちろん、 は
は 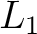 上一次の因数
上一次の因数 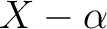 をもつ。
しかし、
をもつ。
しかし、 がこれ以上因数分解できるかどうかは
場合による。
がこれ以上因数分解できるかどうかは
場合による。
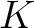 とその上の(既約とは限らない)一変数多項式
とその上の(既約とは限らない)一変数多項式 ![$f\in K[X]$](img9.png) が与えられているとする。このとき、
が与えられているとする。このとき、
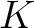 の拡大体
の拡大体 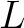 が
が  の分解体であるとは、
の分解体であるとは、 が
が 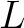 上の多項式として
1次式の積に分解できるときにいう。
上の多項式として
1次式の積に分解できるときにいう。
もっと一般に、 体 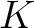 上の有限個の一変数多項式
上の有限個の一変数多項式
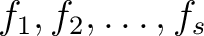 が与えられたとき、
が与えられたとき、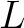 がその分解体
であるとは、各
がその分解体
であるとは、各 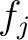 が
が 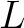 で一次式の積に分解できるようなときにいう。
(これは実際には積
で一次式の積に分解できるようなときにいう。
(これは実際には積
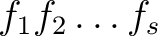 の分解体ということと同じである。)
の分解体ということと同じである。)
与えられた一変数多項式  にたいして、
その分解体は一意とは限らない。じっさい、
にたいして、
その分解体は一意とは限らない。じっさい、
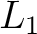 が
が  の分解体なら、
の分解体なら、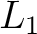 の拡大体はどれも
の拡大体はどれも  の分解体である。
の分解体である。
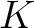 上の任意の一変数多項式
上の任意の一変数多項式  は分解体をもつ。すなわち、
ある体
は分解体をもつ。すなわち、
ある体 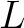 で、
で、 が
が 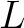 上一次式の積に分解できるようなものが存在する。
上一次式の積に分解できるようなものが存在する。
上の命題を用いると、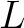 が
が  の分解体であるとは、
の分解体であるとは、
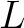 を十分大きい体
を十分大きい体 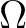 に埋め込んだ時に
に埋め込んだ時に
 の
の 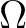 における
における 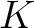 上の共役がすべて
上の共役がすべて 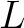 に
含まれているということと同値であるということがわかる。
に
含まれているということと同値であるということがわかる。
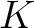 の拡大体
の拡大体 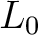 と、その拡大体
と、その拡大体
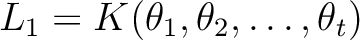 が与えられているとする。
が与えられているとする。
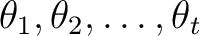 の
の 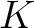 上の最小多項式を
上の最小多項式を
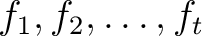 と置こう。
このときもし
と置こう。
このときもし 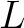 が
が
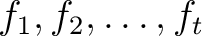 の分解体ならば次のことが成り立つ。
の分解体ならば次のことが成り立つ。
中への 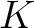 -同型
-同型
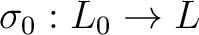 が任意に与えられたとき、
が任意に与えられたとき、
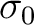 の延長であるような中への同型
の延長であるような中への同型
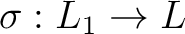 が存在する。
が存在する。
上の定理の条件は 「(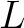 の十分大きな拡大体
の十分大きな拡大体 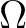 の中で,)
の中で,)
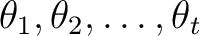 のすべての
のすべての 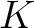 上の
(
上の
(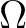 内での)共役が
内での)共役が 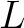 に属する」ということと同値である。
に属する」ということと同値である。
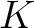 とその上の一変数多項式
とその上の一変数多項式  が与えられたとき、
が与えられたとき、
 の分解体
の分解体 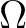 が存在するのであった。
が存在するのであった。
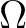 の中での
の中での  の根を
の根を
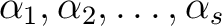 と
おくとき、
と
おくとき、
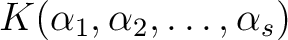 は明らかに
は明らかに
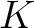 の拡大体で
の拡大体で  の分解体のうち極小なものである。
これを
の分解体のうち極小なものである。
これを  の極小分解体(minimal splitting field)と呼ぼう。
の極小分解体(minimal splitting field)と呼ぼう。上で「間に合わせ的」と書いたのは次のように「最小...」と呼ぶことが 普通だからである。(英語なら the が付くか否かの違いに過ぎない。)
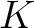 とその上の一変数多項式
とその上の一変数多項式  が与えられたとき、
が与えられたとき、
 の極小分解体はすべて互いに
の極小分解体はすべて互いに 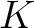 -同型である。
したがってそれらをいちいち区別せずに最小分解体
(the minimal splitting field)と呼ぶ。
-同型である。
したがってそれらをいちいち区別せずに最小分解体
(the minimal splitting field)と呼ぶ。今回のまとめ:
一変数多項式はそれがどんなものであれ体を拡大すれば 一次式の積に分解できるということ、そのために必要な体はどれも 同型であることを学んだ。このことは今後の議論に重要な基礎を与える。
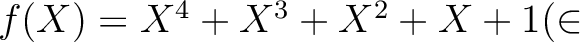

![$[X])$](img26.png) とおく。このとき、
とおく。このとき、
 は
は 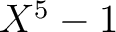 の因数であることを示しなさい。
の因数であることを示しなさい。
 のひとつの根を
のひとつの根を 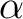 と置くと、
と置くと、
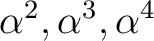 も
も
 の根であることを示しなさい。
の根であることを示しなさい。

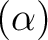 は
は
 上の
上の  の最小分解体であることを
示しなさい。
の最小分解体であることを
示しなさい。
 は
は

![$[X]$](img30.png) の元として既約であることを示しなさい。
(ヒント:
の元として既約であることを示しなさい。
(ヒント:  が既約でなかったとして、
が既約でなかったとして、 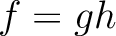 と因数分解されたとする。
と因数分解されたとする。
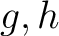 はともにモニックとして良い。前問の結果をもちいて、
はともにモニックとして良い。前問の結果をもちいて、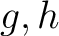 の定数項が
また
の定数項が
また  の根であることを示せ。その結果
の根であることを示せ。その結果  が
が
 上に
解を持つことにするが、これは
上に
解を持つことにするが、これは  の複素数体上の素因数分解の
結果に反する。(
の複素数体上の素因数分解の
結果に反する。( は実数の根をもたない)。
は実数の根をもたない)。