Next: About this document ...
今日のテーマ: 既約性の判定
今回は少しガロア理論の本筋からは外れる。 これまで、個々の例の多項式の既約性について証明なしに議論してきたが、 だんだん不自由になってきたのでここでまとめておくことにする。
代数についてよく学びたい人のための注:
今回の議論は
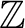 とその商体
とその商体
 に関してのべるが、
一般の UFD
に関してのべるが、
一般の UFD 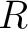 とその商体
とその商体 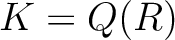 に関しても同様なことが成り立つ。
に関しても同様なことが成り立つ。
次の命題は多項式の既約性判定の際に整数係数と有理係数の差を うまく処理してくれる:
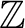 上の多項式
上の多項式
![$f(X) \in {\mbox{${\mathbb{Z}}$}}[X]$](img5.png) が
が
 上で可約ならば、
上で可約ならば、
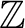 上でも可約である。
上でも可約である。
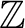 上の多項式
上の多項式
![$f(X) \in {\mbox{${\mathbb{Z}}$}}[X]$](img5.png) が原始的であるとは
が原始的であるとは
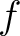 の係数のすべてを割るような整数が
の係数のすべてを割るような整数が 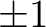 しかないときにいう。
言い換えると、原始的多項式とは係数の gcd が
しかないときにいう。
言い換えると、原始的多項式とは係数の gcd が 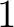 の多項式である。
の多項式である。
![$f,g\in {\mbox{${\mathbb{Z}}$}}[X]$](img9.png) の積
の積 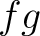 はまた原始的である。
はまた原始的である。
![$h\in {\mbox{${\mathbb{Z}}$}}[X]$](img11.png) が多項式
が多項式
![$f,g\in {\mbox{${\mathbb{Z}}$}}[X]$](img9.png) の積の時、
の積の時、
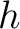 の定数項は
の定数項は 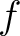 の定数項と
の定数項と 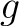 の定数項の積である。
の定数項の積である。
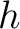 の最高次の係数は
の最高次の係数は 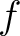 の最高次の係数と
の最高次の係数と 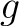 の最高次の係数との
積である。
の最高次の係数との
積である。
![${\mbox{${\mathbb{Z}}$}}[X]$](img14.png) の多項式がもし可約ならばそれはモニックな因数を持つ。
の多項式がもし可約ならばそれはモニックな因数を持つ。
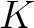 上の 3次もしくは2次の多項式
上の 3次もしくは2次の多項式 ![$f\in K[X]$](img16.png) について、
について、
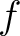 が
が 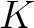 の中に根を持たなければ
の中に根を持たなければ 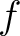 は
は 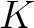 上既約である。
上既約である。
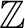 を係数にもつモニックな
を係数にもつモニックな
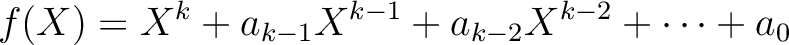
が、ある素数 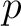 に対して、次の二つの性質をもつとする。
に対して、次の二つの性質をもつとする。
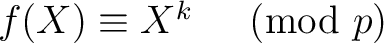
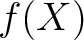 の定数項は
の定数項は 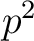 で割り切れない。
で割り切れない。
 は
は
 上既約である。
上既約である。
次のこともよく用いる。
![$f\in k[X]$](img24.png) と任意の定数
と任意の定数 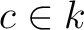 に対して、
に対して、
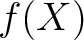 が既約
が既約
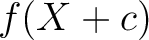 が既約.
が既約.
![$f(X) \in {\mbox{${\mathbb{Z}}$}}[X]$](img5.png) が与えられているとする。
ある素数
が与えられているとする。
ある素数 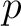 に対して
に対して 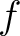 が
が
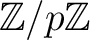 係数の多項式として既約なら、
係数の多項式として既約なら、
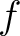 は
は

![$[X]$](img29.png) の元として既約で
ある。
の元として既約で
ある。
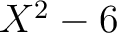 は
は
 上既約であることを示しなさい。
(今回はもちろん
上既約であることを示しなさい。
(今回はもちろん 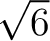 が無理数であることを使ってはならない。)
が無理数であることを使ってはならない。)
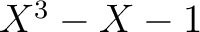 は
は
 上既約であることを示しなさい。
上既約であることを示しなさい。
[根と解]
体 一変数多項式 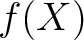 を
を
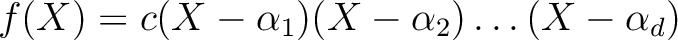
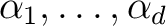 のことを
のことを
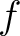 の根と呼ぶ。
の根と呼ぶ。
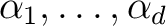 自身は
自身は 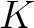 の元でなくても、
の元でなくても、
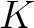 の適当な拡大体(分かりやすいのは、
の適当な拡大体(分かりやすいのは、
 のときの
のときの
 や、
や、
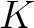 の代数的閉包(後述)
の代数的閉包(後述) 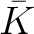 ) の元でよい。
) の元でよい。
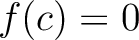 を満たす
を満たす 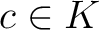 を
を 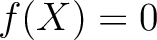 の(
の(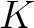 上の)解と呼ぶ。
上の)解と呼ぶ。