Next: About this document ...
今日のテーマ:3次・4次の方程式の解法
3次方程式
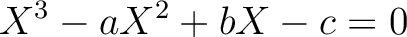
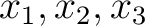 とする。
根が何であるか、具体的に知らないわけだが、その存在は既に知っている。
とする。
根が何であるか、具体的に知らないわけだが、その存在は既に知っている。
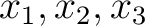 の持つ性質から逆算して、その解き方を見ようというわけだ。
の持つ性質から逆算して、その解き方を見ようというわけだ。
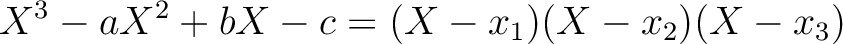 |
(★) |
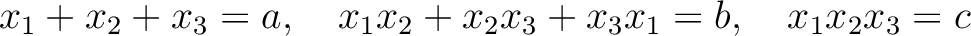
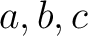 は知っている数だから、
は知っている数だから、
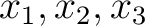 の
基本対称式の値を知っているということになる。
の
基本対称式の値を知っているということになる。
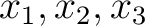 の対称式の値もこれらから(
の対称式の値もこれらから(
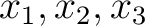 の値を個別に知らなくても)
計算できる。
したがって、如何にして便利な対称式を作るか、が大事になる。
の値を個別に知らなくても)
計算できる。
したがって、如何にして便利な対称式を作るか、が大事になる。
ラグランジュの分解式
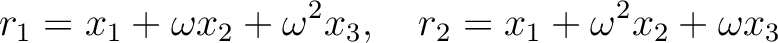 |
(R1) |
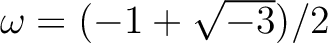 .)
これら自体は
.)
これら自体は
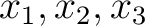 の対称式ではないが、
の対称式ではないが、
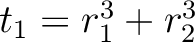 と
と
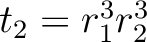 はともに
はともに
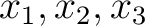 の
対称式である。
の
対称式である。
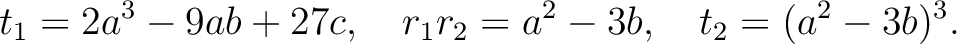
このことから、
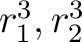 を二次方程式
を二次方程式
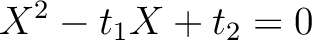
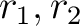 を計算できる。
そこから
を計算できる。
そこから
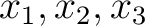 を
出すのは連立一次方程式を解けばよい(ラグランジュの分解式二つと
根と係数の関係の一番目の式)ので簡単である。
を
出すのは連立一次方程式を解けばよい(ラグランジュの分解式二つと
根と係数の関係の一番目の式)ので簡単である。
4次方程式の場合を考えよう。
根を
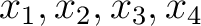 とおくと、
とおくと、
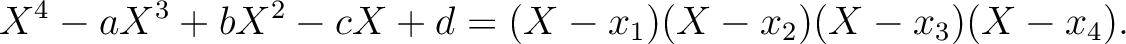
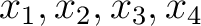 の
対称式は
の
対称式は 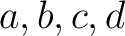 から(
から(
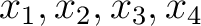 の値を知らなくても)
計算できる。
の値を知らなくても)
計算できる。
ラグランジュの分解式として、
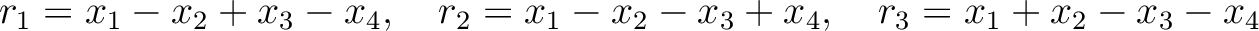
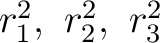 の基本対称式
の基本対称式
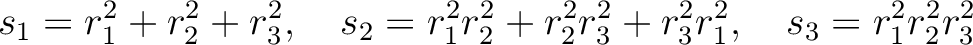
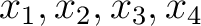 の対称式になっていることが分かり、したがって
の対称式になっていることが分かり、したがって 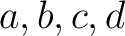 から計算できる。
すなわち、
から計算できる。
すなわち、
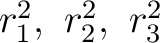 は
は
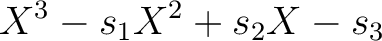
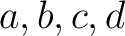 から計算できる。
あとはその平方根を計算すれば、
から計算できる。
あとはその平方根を計算すれば、
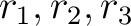 が計算されて、
一次方程式の根として
が計算されて、
一次方程式の根として
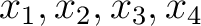 が計算されるという仕組である。
が計算されるという仕組である。
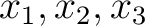 の置換(6つある)によって(R1)の分解式
の置換(6つある)によって(R1)の分解式 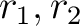 が
それぞれどのように変化するか、実際に書き下しなさい。
が
それぞれどのように変化するか、実際に書き下しなさい。