Next: About this document ...
今日のテーマ:行列式(2)
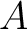 が与えられた時、その
が与えられた時、その 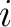 行と
行と 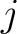 列を引っこ抜き,
その行列式をとって
ついでに符号
列を引っこ抜き,
その行列式をとって
ついでに符号
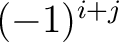 をつけたものを
をつけたものを 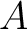 の余因子
(より正確には、
の余因子
(より正確には、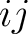 -余因子)といい、
-余因子)といい、
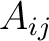 で書き表す。
で書き表す。
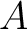 の
の 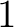 列目が基本列ベクトル
列目が基本列ベクトル
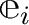 に等しいならば、
に等しいならば、
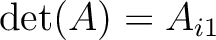 .
.
(もっと一般に、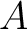 の
の 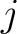 列目が
列目が
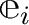 に等しいならば、
に等しいならば、
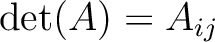 .)
.)
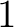 行目に関する展開)
任意の
行目に関する展開)
任意の 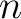 次正方行列
次正方行列
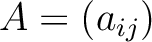 に対して、
に対して、
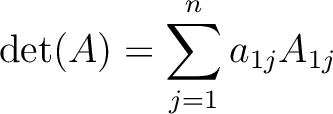
上の命題と同様にして、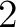 行目、
行目、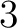 行目,...
行目,... 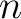 行目に関する展開が
得られる。
行目に関する展開が
得られる。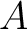 を、「
を、「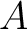 の
の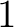 列目を
列目を 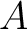 の
の 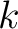 列目に置き換えた行列」
に置き換えることにより、つぎの結果を得ることができる。
列目に置き換えた行列」
に置き換えることにより、つぎの結果を得ることができる。
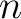 次正方行列
次正方行列
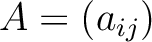 に対して、
に対して、
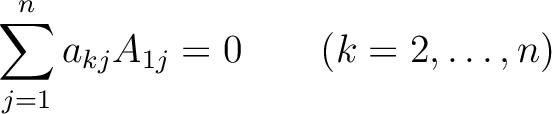
これもまた、 行目だけについて特別に言えることではなく、結局次のことが言える:
行目だけについて特別に言えることではなく、結局次のことが言える:
 次正方行列
次正方行列
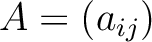 に対して、
に対して、
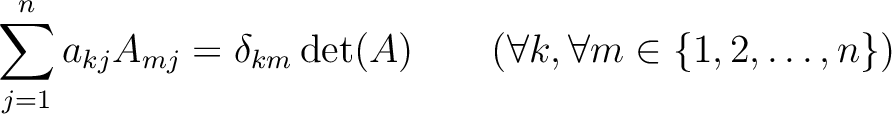
この式は次のことを意味している:
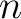 次正方行列
次正方行列
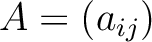 に対して、
各
に対して、
各 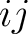 成分が
成分が 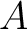 の余因子
の余因子 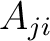 であるような行列
(
であるような行列
(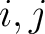 の順番に注意。)を
の順番に注意。)を 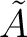 と書くことにする。
(
と書くことにする。
(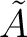 のことを
のことを 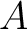 の余因子行列とよぶ。)
このとき、
の余因子行列とよぶ。)
このとき、
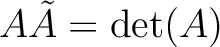
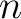 次正方行列
次正方行列 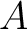 が逆行列を持つことと、
が逆行列を持つことと、
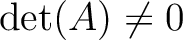 とは同値である。
とは同値である。