Next: About this document ...
今日のテーマ :行列式 (3) 余因子と逆行列
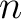 次正方行列
次正方行列 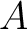 を
を
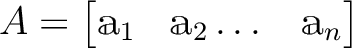 とブロック分割する。
とブロック分割する。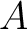 の行列式
の行列式
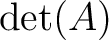 を、
以下では
を、
以下では 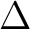 と書くことにする。
いま、
と書くことにする。
いま、 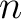 次元縦ベクトル
次元縦ベクトル
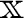 を
を
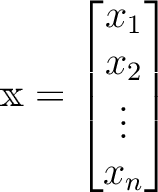
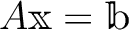 ならば、
ならば、
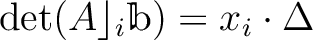
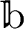 がはじめに与えられて、
がはじめに与えられて、
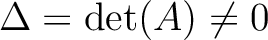 ならば、
ならば、
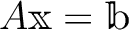 の解は
の解は

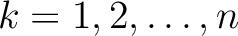 にたいして、
にたいして、
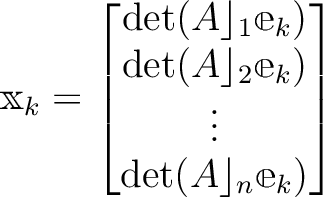
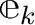 は
は 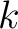 番目の基本ベクトル)。
すると、
番目の基本ベクトル)。
すると、
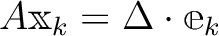 である。
である。
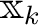 をならべて
をならべて
![$\displaystyle A[\mathbbm x_1 \mathbbm x_2 \dots \mathbbm x_n]= \Delta \cdot E_n
$](img19.png)
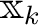 にたいして、
にたいして、
![$[\mathbbm x_1 \mathbbm x_2 \dots \mathbbm x_n]$](img20.png) は
は 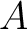 の余因子行列と等しい。
の余因子行列と等しい。
行列の逆行列の行列式による表示、クラーメルの公式は、 計算量的にはいまいちである。が、次のような利点がある。 (クラーメルの公式でも同じなので逆行列についてのみ述べる。)
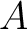 の逆行列は
の逆行列は
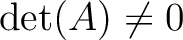 である限り
である限り 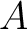 について
連続的に動く。
について
連続的に動く。
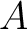 の逆行列の各成分は、
の逆行列の各成分は、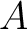 の成分の和、差、積を適当にとったあと、
の成分の和、差、積を適当にとったあと、
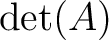 で割ることで得られる。(それ以外の演算は必要ない)
で割ることで得られる。(それ以外の演算は必要ない)
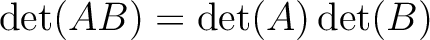 が任意の
が任意の
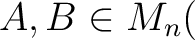
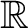
 に対して
成り立つ。
に対して
成り立つ。