Next: About this document ...
今日のテーマ: ベクトル(2)
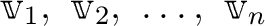 が一次従属であるとは、非自明な1次の関係式
が一次従属であるとは、非自明な1次の関係式
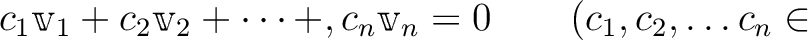
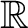
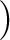
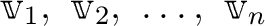 が一次従属でない時、一次独立であるという。
が一次従属でない時、一次独立であるという。
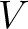 の元
の元
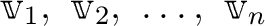 が
が 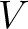 の基底であるとは、次の2つのことが成り立つときにいう。
の基底であるとは、次の2つのことが成り立つときにいう。
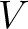 の任意の元は
の任意の元は
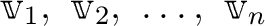 の
線型結合で書ける。
の
線型結合で書ける。
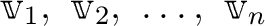 は
一次独立である。
は
一次独立である。
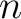 個の元からなる基底が存在するようなベクトル空間を
個の元からなる基底が存在するようなベクトル空間を 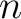 次元ベクトル空間という。
次元ベクトル空間という。
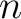 次元ベクトル空間
次元ベクトル空間 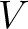 をとろう。定義により
をとろう。定義により 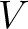 には
には 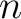 個の
元からなる基底
個の
元からなる基底
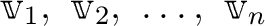 が存在する。
が存在する。
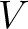 の元
の元
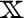 は
は
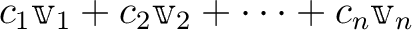 と
書くことができる。
と
書くことができる。
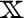 に数ベクトル
に数ベクトル
![$[c_1,\dots,c_n]$](img9.png) を対応させることで、
を対応させることで、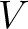 を具体的な空間
を具体的な空間
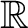
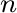 と同一視できる。
と同一視できる。
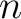 次元計量ベクトル空間
次元計量ベクトル空間 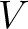 については、次のような基底が存在する。
(正規直交基底)
については、次のような基底が存在する。
(正規直交基底)
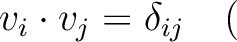 クロネッカーのデルタ
クロネッカーのデルタ
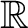 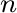 |
|
基底
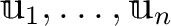 |
基本ベクトル
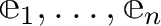 |
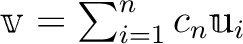 |
![$[c_1,c_2,\dots,c_n] $](img16.png) |
| 内積 |
![$[c_1,c_2,\dots,c_n]\cdot [c_1',\dots,c_n']=\sum_{i=1}^n c_i c_i' $](img17.png) |