Next: About this document ...
今日のテーマ: 行列の対角化。
 次正方行列
次正方行列 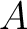 の固有値
の固有値
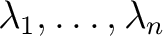 の固有ベクトル
の固有ベクトル
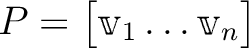 に対して、
に対して、
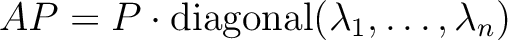 が成り立つ。とくに
が成り立つ。とくに
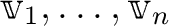 が、一次独立ならば、
が、一次独立ならば、
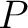 は可逆で、
は可逆で、
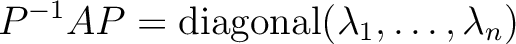
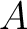 の対角化という。
の対角化という。
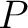 を
を 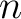 次の正方行列、
次の正方行列、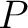 は可逆だとする。
このとき、任意の
は可逆だとする。
このとき、任意の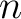 次正方行列
次正方行列 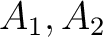 に対して次のことがなりたつ。
に対して次のことがなりたつ。
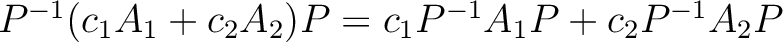 .
(
.
(
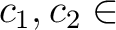
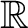 ).
).
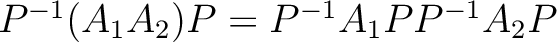 .
.
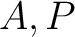 を
を 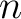 次の正方行列、
次の正方行列、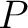 は可逆だとする。
は可逆だとする。
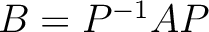 とおくとき、
とおくとき、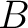 が対角行列であるか否かにかかわらず、
が対角行列であるか否かにかかわらず、
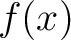 に対して、
に対して、
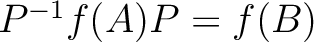
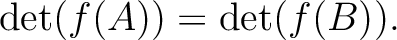 .
.
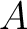 の固有多項式と
の固有多項式と 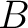 の固有多項式は等しい。
の固有多項式は等しい。
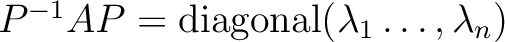 のときには、
のときには、
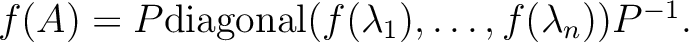 .
.
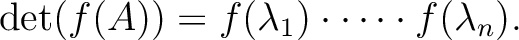
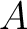 の固有多項式は
の固有多項式は
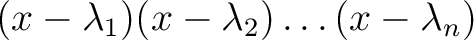 と等しい。
と等しい。
*上の命題の極限を考えることにより、行列の
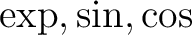 も
同様に計算することができる。これは微分方程式の解法などでとくに有用である。
も
同様に計算することができる。これは微分方程式の解法などでとくに有用である。
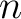 次正方行列
次正方行列 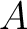 の固有値
の固有値
 の固有ベクトル
の固有ベクトル
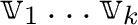 があったとする。もし、
があったとする。もし、
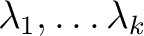 がどれも異なれば、
がどれも異なれば、
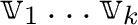 は一次独立である。
は一次独立である。
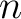 次正方行列
次正方行列 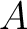 の
の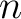 個の固有値が実数で、互いに相異なれば、
個の固有値が実数で、互いに相異なれば、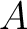 は
対角化可能である。
は
対角化可能である。*話を複素数にまで拡張しておくと、つぎのように単純化される。
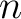 次複素正方行列
次複素正方行列 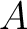 の
の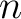 個の固有値が互いに相異なれば、
個の固有値が互いに相異なれば、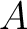 は
対角化可能である。
は
対角化可能である。
*
行列
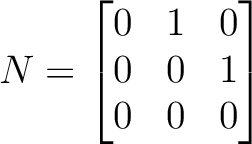 の固有値は
の固有値は 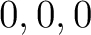 で、固有ベクトルは
で、固有ベクトルは
![${}^t [1,0,0]$](img30.png) の
一つだけである。よって
の
一つだけである。よって 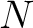 は対角化できない。
は対角化できない。
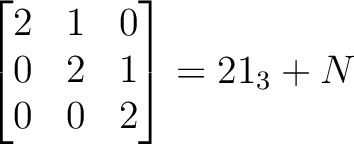 の固有値は
の固有値は 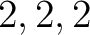 で、対角化できない。
一般の、対角化不可能な行列については、座標変換で「ジョルダンの標準形」までは
持っていくことができる。詳しくは線形代数の進んだ成書を参考のこと。
で、対角化できない。
一般の、対角化不可能な行列については、座標変換で「ジョルダンの標準形」までは
持っていくことができる。詳しくは線形代数の進んだ成書を参考のこと。
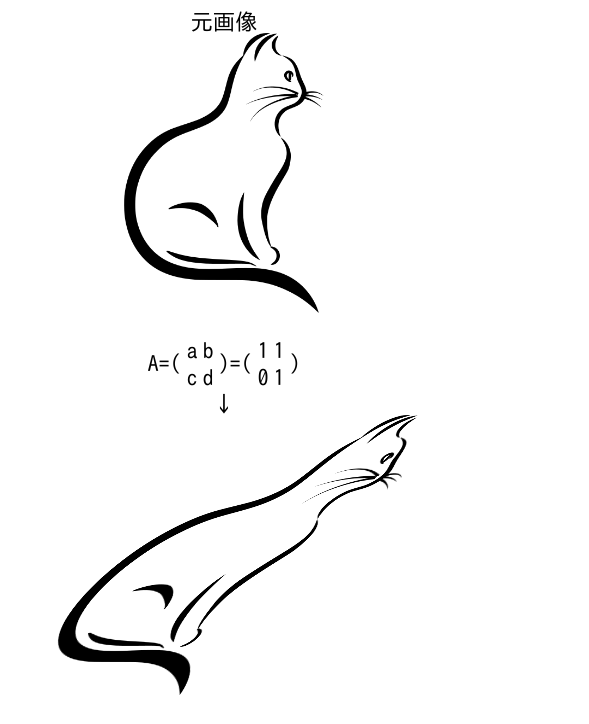
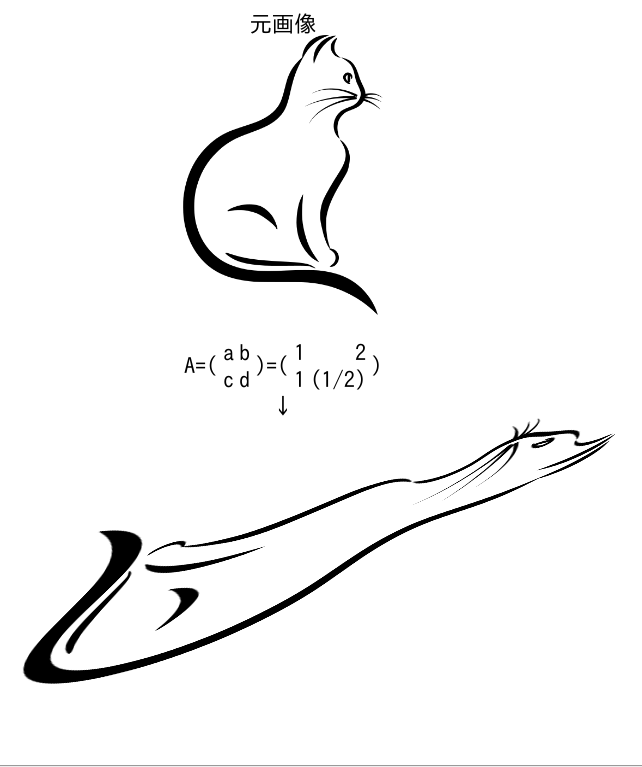
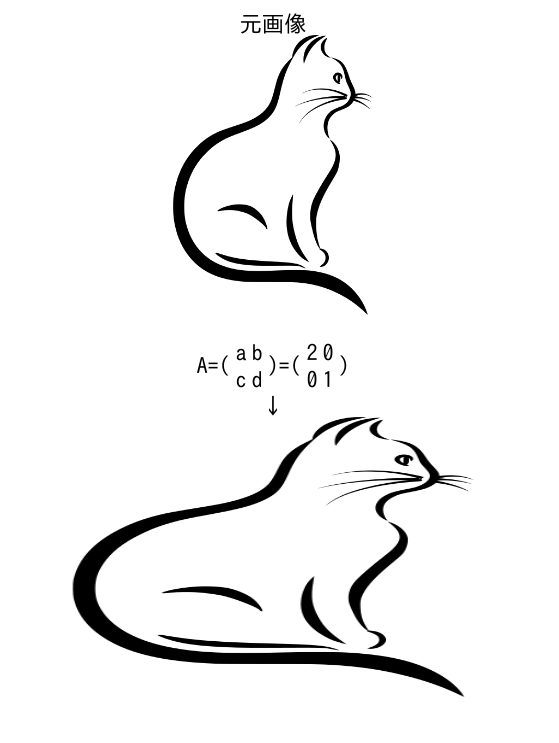
いくつかの猫の絵を線形変換で移してみた。 (猫の絵は
https://pixabay.com/vectors/cat-cool-remeras-helical-helix-1294968/
から借用。ライセンスはそちらを参照のこと)