Next: About this document ...
 《環の準同型定理(2)》
《環の準同型定理(2)》
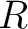 から別の環
から別の環 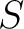 への準同型写像
への準同型写像
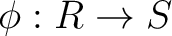 が与えられたとする。
このとき、次が成り立つ。
が与えられたとする。
このとき、次が成り立つ。
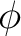 の像
の像
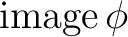 は
は 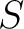 の部分環である。
の部分環である。
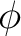 の核
の核
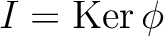 は
は 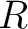 のイデアルである。
のイデアルである。
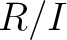 は
は
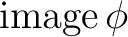 と同型である。
と同型である。
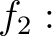

![$[X]\to {\mathbb{C}}$](img11.png) を
を
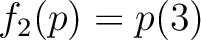 で定義する。
で定義する。
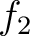 は環準同型であり、環の準同型定理により
環の同型
は環準同型であり、環の準同型定理により
環の同型
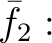

![$\displaystyle [X]/(X-3)\cong$](img16.png)

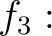

![$[X]\to {\mathbb{C}}$](img11.png) を
を
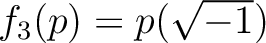 で定義する。
で定義する。
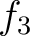 は環準同型であり、環の準同型定理により
環の同型
は環準同型であり、環の準同型定理により
環の同型
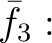

![$\displaystyle [X]/(X^2+1)\cong$](img21.png)

![% latex2html id marker 1091
$\displaystyle [\sqrt{-1}]
$](img22.png)
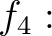
![$[X]\to {\mathbb{C}}$](img11.png) を
を
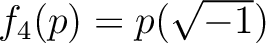 で定義する。
で定義する。
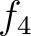 は環準同型であり、環の準同型定理により
環の同型
は環準同型であり、環の準同型定理により
環の同型
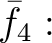
![$\displaystyle [X]/(X^2+1)\cong {\mathbb{C}}
$](img29.png)
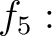

![$[X]\to {\mathbb{C}}$](img11.png) を
を
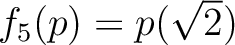 で定義する。
で定義する。
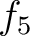 は環準同型であり、環の準同型定理により
環の同型
は環準同型であり、環の準同型定理により
環の同型
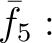

![$\displaystyle [X]/(X^2-2)\cong$](img34.png)

![% latex2html id marker 1127
$\displaystyle [\sqrt{2}]
$](img35.png)
![$f_6:{\mbox{${\mathbb{Z}}$}}[X]\to {\mathbb{C}}$](img36.png) を
を
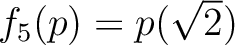 で定義する。
で定義する。
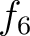 は環準同型であり、環の準同型定理により
環の同型
は環準同型であり、環の準同型定理により
環の同型
![% latex2html id marker 1140
$\displaystyle \bar{f_6}: {\mbox{${\mathbb{Z}}$}}[X]/(X^2-2)\cong {\mbox{${\mathbb{Z}}$}}[\sqrt{2}]
$](img39.png)
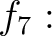

![$[X,Y]\to {\mathbb{C}}$](img41.png) を
を
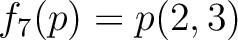 で定義する。
で定義する。
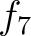 は環準同型であり、環の準同型定理により
環の同型
は環準同型であり、環の準同型定理により
環の同型
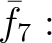

![$\displaystyle [X,Y]/(X-2,Y-3)\cong$](img45.png)

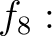

![$[X,Y]\to {\mathbb{C}}$](img41.png) を
を
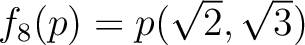 で定義する。
で定義する。
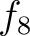 は環準同型であり、環の準同型定理により
環の同型
は環準同型であり、環の準同型定理により
環の同型
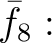

![$\displaystyle [X]/(X^2-2,Y^2-3)\cong$](img50.png)

![% latex2html id marker 1177
$\displaystyle [\sqrt{2},\sqrt{3}]
$](img51.png)
今回の例で、

![% latex2html id marker 1180
$ [\sqrt{-1}],({\mathbb{C}}),$](img52.png)

![% latex2html id marker 1182
$ [\sqrt{2}],$](img53.png)

![% latex2html id marker 1184
$ [\sqrt{2},\sqrt{3}]$](img54.png) は体である。その意味で、例えば
は体である。その意味で、例えば

![% latex2html id marker 1187
$ [\sqrt{-1}]$](img55.png) のことを「
のことを「
 に
に 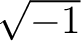 を付け加えた体」とよび、
を付け加えた体」とよび、

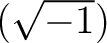 と書いたりする。
これは体論において基本的な構成である。
と書いたりする。
これは体論において基本的な構成である。