Next: About this document ...
 整域における整除の問題
整域における整除の問題
環論においては、元 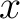 の性質を調べる代わりに、
の性質を調べる代わりに、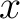 の生成するイデアル
の生成するイデアル 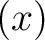 を調べるとうまくいくことがある。
とくに整除の問題はイデアルの包含関係に翻訳される。
を調べるとうまくいくことがある。
とくに整除の問題はイデアルの包含関係に翻訳される。
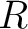 は環であるとする。
は環であるとする。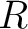 の元のうち、
積に関して可逆なものを
の元のうち、
積に関して可逆なものを 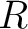 の可逆元と言い、
その全体を
の可逆元と言い、
その全体を 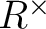 であらわす。
であらわす。
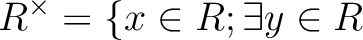 に対して
に対して 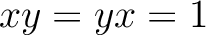 が成り立つ
が成り立つ
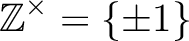 ,
,
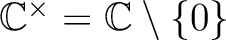 ,
,
![${\mathbb{C}}[X]^\times={\mathbb{C}}^\times$](img11.png) .
.
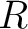 の元
の元 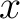 について、次は同値である。
について、次は同値である。
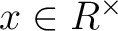
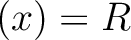
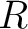 と
と 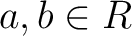 とにたいして、
とにたいして、
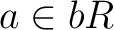 のとき、
のとき、 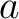 は
は 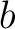 の (
の (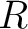 における)倍元であるといい、
における)倍元であるといい、
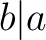 で書き表す。
で書き表す。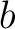 を主語として、
を主語として、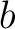 は
は 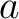 の (
の (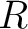 における)
約元であるともいう。
における)
約元であるともいう。
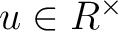 があって、
があって、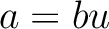 をみたすとき、
をみたすとき、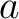 と
と 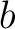 とは
(
とは
(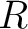 において)
同伴であるという。
において)
同伴であるという。
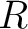 の元
の元 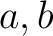 にたいして、
にたいして、
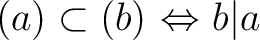 .
.
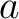 と
と 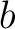 が同伴
が同伴
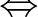
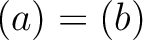 .
.
 が与えられているとする。
が与えられているとする。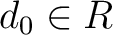 が
が 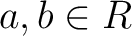 の
最大公約元(
の
最大公約元(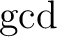 ) であるとは
) であるとは
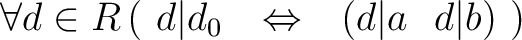
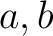 の最大公約元がもし存在すれば、それを
の最大公約元がもし存在すれば、それを 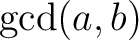 と書く。
と書く。
定義を追っかけていくと、すぐに次のことがわかる。
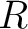 が与えられているとする。
が与えられているとする。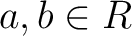 に対して、
に対して、
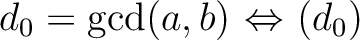 は
は 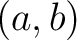 を含む単項イデアルの中で最小。
を含む単項イデアルの中で最小。
とくに、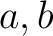 の最大公約数は同伴を除いて一意的である。
の最大公約数は同伴を除いて一意的である。
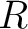 の元
の元 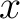 が素元であるとは、
が素元であるとは、
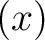 が
が 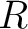 の素イデアルであるときにいう。
の素イデアルであるときにいう。

![% latex2html id marker 1064
$ R= {\mbox{${\mathbb{Z}}$}}[\sqrt{-5}] $](img32.png) では
では
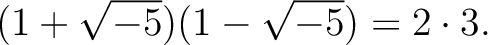
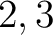 は(
は(
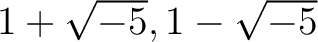 も)
それぞれ
も)
それぞれ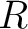 の素元ではないことがわかる。
ところが、これらの数は
の素元ではないことがわかる。
ところが、これらの数は 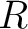 ではこれ以上分解できない(次回。)
ではこれ以上分解できない(次回。)
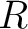 では「素因数分解の一意性」が成り立たないのである。
では「素因数分解の一意性」が成り立たないのである。