Next: About this document ...
言うまでもないことだが、数値的な答だけでは十分ではない。 論理的な説明がもっと大事である。
今年度は一変数多項式の既約性の話をしなかったので、(難)のところは 正しいと仮定しないと辛いだろう。
 とし、
とし、 の根の一つを
の根の一つを  とおく。
とおく。

![$[X]$](img5.svg) から
から

![$[\alpha]$](img6.svg) への環準同型写像
への環準同型写像  を
を
 となるように決める。このとき、
となるように決める。このとき、


![$[X]$](img5.svg) に対して、
に対して、
 を求めよ。
を求めよ。
 であることを示しなさい。
であることを示しなさい。
 は
は

![$[X]$](img5.svg) の既約元であることを示しなさい。
の既約元であることを示しなさい。
 の元は必ず
の元は必ず  で割り切れることを示しなさい。
で割り切れることを示しなさい。
 に対して準同型定理を適用し、得られる環の同型を書きなさい。
に対して準同型定理を適用し、得られる環の同型を書きなさい。
![% latex2html id marker 859
$ \beta=\sqrt[3]{6}$](img1.png) とおく。
とおく。

![$[X]$](img5.svg) から
から

![$[\beta]$](img2.png) への環準同型写像
への環準同型写像  を
を
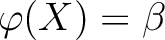 となるように決める。このとき、
となるように決める。このとき、


![$[X]$](img5.svg) に対して、
に対して、
 を求めよ。
を求めよ。
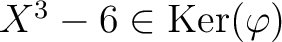 であることを示しなさい。
であることを示しなさい。
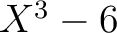 は
は

![$[X]$](img5.svg) の既約元であることを示しなさい。
の既約元であることを示しなさい。
 の元は必ず
の元は必ず 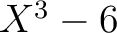 で割り切れることを示しなさい。
で割り切れることを示しなさい。
 に対して準同型定理を適用し、得られる環の同型を書きなさい。
に対して準同型定理を適用し、得られる環の同型を書きなさい。