Next: About this document ...
今日のテーマ: 授業の目標, ベクトル空間及び線形写像の復習。
「スカラー」の集合を一つ決めておかなければならない。
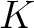 が体であるとは、
が体であるとは、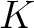 が和、差、積、商について
閉じた集合であるときにいう。
詳しくいうと
が和、差、積、商について
閉じた集合であるときにいう。
詳しくいうと 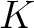 が体であるとは、
が体であるとは、
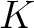 が和(+)、積2つの演算について閉じていて、以下の条件を満たすときに言う。
詳しくは体論でやる。
が和(+)、積2つの演算について閉じていて、以下の条件を満たすときに言う。
詳しくは体論でやる。
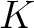 は和について可換群である。
すなわち
は和について可換群である。
すなわち
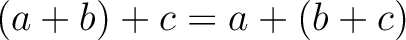
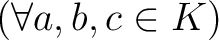 .
.
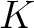 には
には 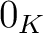 と呼ばれる特別の元があって、
と呼ばれる特別の元があって、
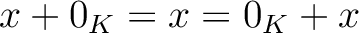
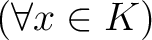 がなりたつ。
がなりたつ。
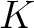 の任意の元
の任意の元
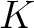 は積について可換半群である。つまり、
結合法則
は積について可換半群である。つまり、
結合法則
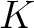 には
には 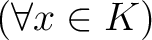 がなりたつ。
がなりたつ。
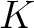 の任意の元
の任意の元
本講義では 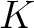 としては
としては
![]() をよく用いるが、
をよく用いるが、
![]() の場合を考えることも時には必要である。
の場合を考えることも時には必要である。
![]()
![]() としたときのベクトル空間を
としたときのベクトル空間を
![]() 上のベクトル空間とか、
実ベクトル空間といい、
上のベクトル空間とか、
実ベクトル空間といい、
![]() としたときのベクトル空間を
としたときのベクトル空間を
![]() 上のベクトル空間とか、複素ベクトル空間と呼ぶ。
上のベクトル空間とか、複素ベクトル空間と呼ぶ。
ベクトル空間とは、その中で和とスカラー倍ができるような集合のことである。 ただし和とスカラー倍は次の法則を満たす必要がある。
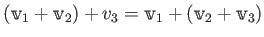 (
(
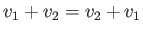 .
.
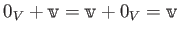 ).
).
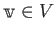 such that
such that
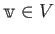 .
.
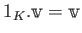 .
.
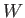
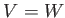
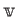
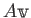
ベクトル空間 ![]() にたいして、
にたいして、![]() から
から ![]() への線形写像とは、
への線形写像とは、
![]() から
から ![]() の写像であって、和とスカラー倍を保つもののことである。
の写像であって、和とスカラー倍を保つもののことである。
![]() ,
,![]() の基底をとることで、線形写像は行列で表せるのであった。
行列としては何でもありうるわけだが、
基底のとり方を上手に選べば、簡単な行列を扱うだけで済むようにできる
場合がある。
の基底をとることで、線形写像は行列で表せるのであった。
行列としては何でもありうるわけだが、
基底のとり方を上手に選べば、簡単な行列を扱うだけで済むようにできる
場合がある。
とくに、![]() の場合が本講義の主題である。
この場合には、
の場合が本講義の主題である。
この場合には、
![]() と
と
![]() とを比較できるということが一般の場合と異なる。
とを比較できるということが一般の場合と異なる。
一番基本的なのは対角行列である。

本講義では、次のようなことについて学ぶ: