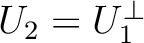Next: About this document ...
今日のテーマ: 直交補空間
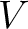 の部分空間
の部分空間 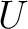 に対して、
に対して、
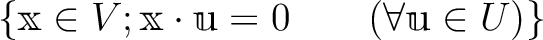
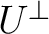 と書き、
と書き、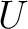 の直交補空間と呼ぶ。
の直交補空間と呼ぶ。
計量ベクトル空間 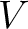 の部分空間
の部分空間 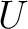 に対して、
に対して、
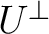 は
は
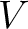 の部分空間である。
の部分空間である。
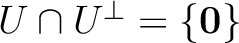 .
.
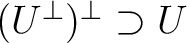 .
.
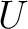 が有限次元なら、
が有限次元なら、
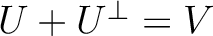 .
したがって(上のことと併せて)
.
したがって(上のことと併せて)
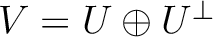 である。
である。
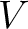 の部分空間
の部分空間 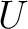 に対して、
に対して、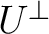 が
有限次元であれば、
が
有限次元であれば、
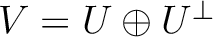 であることを示しなさい。
であることを示しなさい。
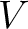 の部分空間
の部分空間 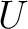 が、
が、
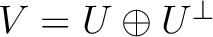 をみたすと仮定する。このとき、
任意の
をみたすと仮定する。このとき、
任意の
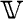 は一意的に
は一意的に
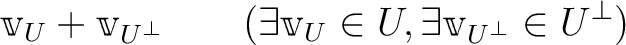
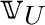 のことは
のことは 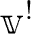 ,
,
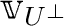 のことは
のことは
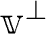 と書かれている。)
と書かれている。)
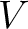 とそのベクトル
とそのベクトル
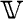 に対して、
に対して、
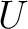 を
を
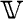 で生成される一次元ベクトル空間に採ると
で生成される一次元ベクトル空間に採ると
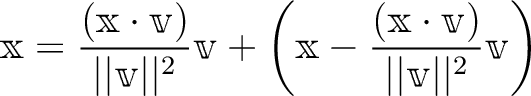
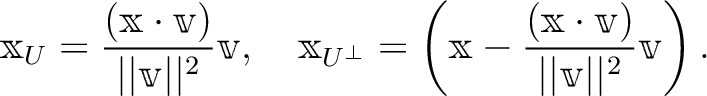
一次独立なベクトルの有限列
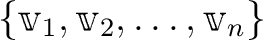 からはじめて、
からはじめて、
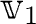 を上記の
を上記の
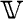 として上記操作を行い、
として上記操作を行い、
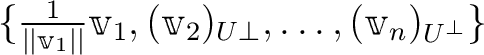 を考えると一番目のベクトルに関して「きれいな」ベクトルの列を得る。
これを繰り返すことにより正規直交系を得るのがシュミットの直交化法である。
を考えると一番目のベクトルに関して「きれいな」ベクトルの列を得る。
これを繰り返すことにより正規直交系を得るのがシュミットの直交化法である。
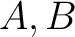 について、
について、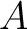 のどの元も
のどの元も 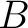 の
各元と直交する時、
の
各元と直交する時、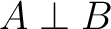 と書く。
すなわち、
と書く。
すなわち、
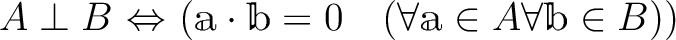
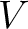 は有限次元の計量ベクトル空間であるとする。このとき、
は有限次元の計量ベクトル空間であるとする。このとき、
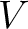 の部分空間
の部分空間 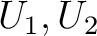 にたいして、つぎは同値である。
にたいして、つぎは同値である。
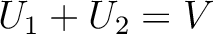 かつ
かつ
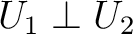 .
.