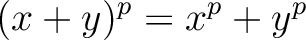Next: Finite fields
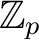 ,
,
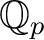 , and the ring of Witt vectors
, and the ring of Witt vectorsYoshifumi Tsuchimoto
You should know that every positive integer may be written in decimal notation:
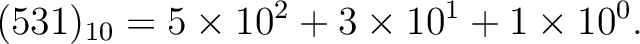
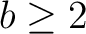 ,
we may write a number as a string of digits in base
,
we may write a number as a string of digits in base 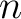 .
For example, we have
.
For example, we have
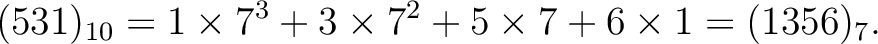
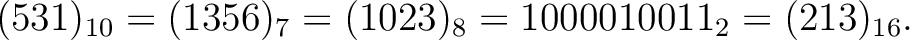
You may also probably know (repeating) decimal expresions of positive rational numbers.
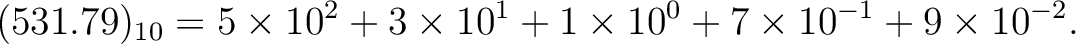
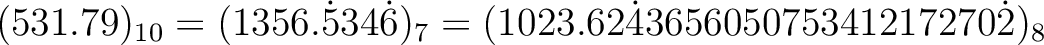
Now let us reverse the order of digits. Namely, we employ a notation like this1:
![$\displaystyle [97.135]_{10}=(531.79)_{10}$](img11.png) | ||
![$\displaystyle [0.135]_{10}=(531)_{10}$](img12.png) | ||
![$\displaystyle [123.456]_{10}=(654.321)_{10}$](img13.png) | ||
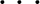 |
Let us do some calculation with the above notation:
![$\displaystyle [0.1]_{10}+ [0.9]_{10}=[0.01]_{10}$](img15.png) | ||
![$\displaystyle [0.1]_{10}\times [0.9]_{10}=[0.9]_{10}$](img16.png) | ||
![$\displaystyle [0.01]_{10}\times [0.09]_{10}=[0.009]_{10}$](img17.png) |
![$\displaystyle [0.12345]_8+[0.75432]_8
$](img18.png)
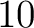 .
.
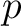 ,
,
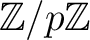 is a field.
(We denote it by
is a field.
(We denote it by
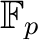 .)
.)
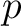 be a prime number.
Let
be a prime number.
Let 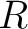 be a commutative ring which contains
be a commutative ring which contains
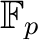 as a subring.
Then we have the following facts.
as a subring.
Then we have the following facts.
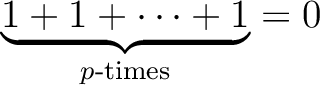
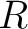 .
.
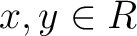 , we have
, we have