Next:
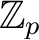 ,
,
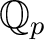 , and the ring of Witt vectors
, and the ring of Witt vectors
From here on, we make use of several notions of category theory. Readers who are unfamiliar with the subject is advised to see a book such as [1] for basic definitions and first properties.
Let 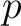 be a prime number.
For any commutative ring
be a prime number.
For any commutative ring 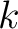 of characteristic
of characteristic 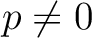 , we want to
construct a ring
, we want to
construct a ring 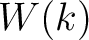 of characteristic 0 in such a way that:
of characteristic 0 in such a way that:
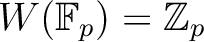 .
.
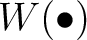 is a functor. That means,
is a functor. That means,
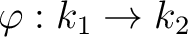 between rings of characterisic
between rings of characterisic 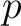 ,
there is given a unique ring homomorphism
,
there is given a unique ring homomorphism
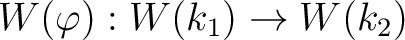 .
.
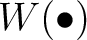 should furthermore
commutes with compositions of homomorphisms.
should furthermore
commutes with compositions of homomorphisms.
Recent days, it gets easier for us on the net to i find some good articles concerning the ring of Witt vectors. The treatment here borrows some ideas from them. See for example the “comments” section in https://www.encyclopediaofmath.org/index.php/Witt_vector