Next: homomorphisms of (pre)sheaves Up: , , and the Previous: sheaves
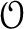 is a sheaf on
is a sheaf on
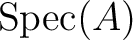 , we may
easily use the arguments we have used to proved
the locality and the gluing lemma.
, we may
easily use the arguments we have used to proved
the locality and the gluing lemma.
For example, the proof we gave in Theorem 7.16,
especially the part where we chose the idempotent 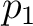 , was a bit complicated.
, was a bit complicated.
Let us give another proof using the sheaf arguments.
There exists a unique element
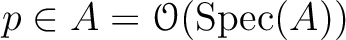 which coincides with
which coincides with 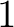 on
on 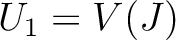 and with 0 on
and with 0 on 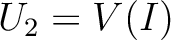 .
From the uniqueness we see that
.
From the uniqueness we see that
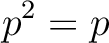
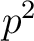 satisfies the same properties as
satisfies the same properties as 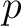 .
The rest of the proof is the same.
.
The rest of the proof is the same.
As a second easier example, we consider the following undergraduate problem.
Problem: Find the inverse of the matrix
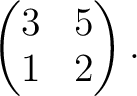
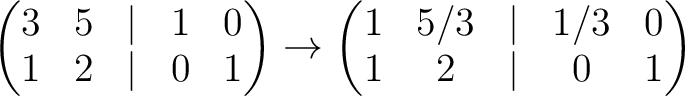 | ||
 |
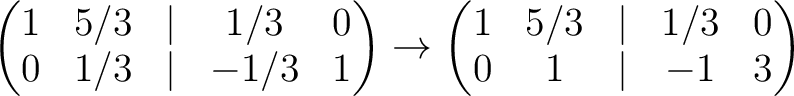 | |
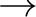 |
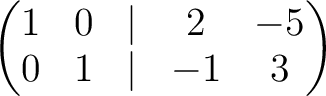 |
The calculation is valid on
![$\operatorname{Spec}(\mathbb{Z}[1/3])$](img249.png) .
.
Another student may calculate (using “operations on columns”) as follows.
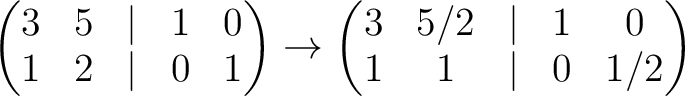 | ||
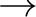 |
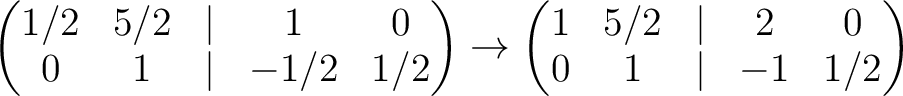 | |
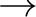 |
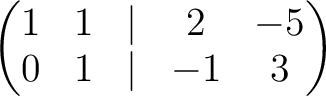 |
The calculation is valid on
![$\operatorname{Spec}(\mathbb{Z}[1/2])$](img253.png) .
Of course, both calculations are valid on the intersection
.
Of course, both calculations are valid on the intersection
![$\operatorname{Spec}(\mathbb{Z}[1/2])\cap \operatorname{Spec}(\mathbb{Z}[1/3])=\operatorname{Spec}(\mathbb{Z}[1/6])$](img254.png) .
.
The gluing lemma asserts that the answer obtained individually is automatically an answer on
the whole of
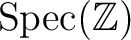 .
Of course, in this special case, there are lots of easier ways to
tell that. But one may imagine this kind of thing is helpful when
we deal with more complicated objects.
.
Of course, in this special case, there are lots of easier ways to
tell that. But one may imagine this kind of thing is helpful when
we deal with more complicated objects.