Next: general localization of a Up: , , and the Previous: stalk of a presheaf
In this subsection we restrict ourselves to deal with sheaves of modules.
To shorten our statements, we call a presheaf which satisfies (only) the sheaf axiom (1) (locality) a “(1)-presheaf”.
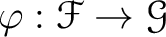 be a homomorphism between sheaves of
modules. Then we have
be a homomorphism between sheaves of
modules. Then we have
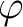 is a sheaf.
We call it the sheaf kernel
is a sheaf.
We call it the sheaf kernel
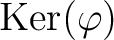 of
of 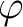 .
.
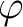 is not necessarily a sheaf,
but it is a (1)-presheaf.
We call the sheafication of the presheaf image as the sheaf image
is not necessarily a sheaf,
but it is a (1)-presheaf.
We call the sheafication of the presheaf image as the sheaf image
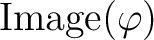 of
of 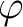 .
.
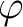 is not necessarily a sheaf.
We call the sheafication of the cokernel as the sheaf cokernel
is not necessarily a sheaf.
We call the sheafication of the cokernel as the sheaf cokernel
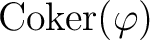 of
of 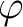 .
.
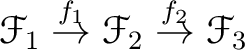
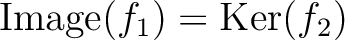 holds.
holds.
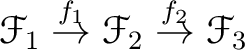
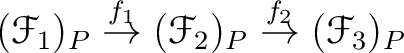
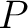 .
.