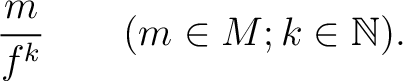Next: Existence of a point Up: , , and the Previous: ring homomorphism and spectrum
 be an element of a commutative ring
be an element of a commutative ring  . Then we define the
localization
. Then we define the
localization 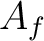 of
of 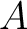 with respect to
with respect to 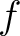 as a ring defined by
as a ring defined by
![$\displaystyle A_{f}=A[X]/(X f -1)
$](img39.png)
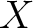 is a indeterminate.
is a indeterminate.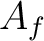 , the residue class of
, the residue class of 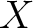 plays the role of the
inverse of
plays the role of the
inverse of 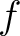 . Therefore, we may write
. Therefore, we may write ![$A[1/f]$](img41.png) instead of
instead of 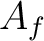 if there is no confusion.
if there is no confusion.
One may define localization in much more general situation. The reader is advised to read standard books on commutative algebras.
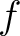 be an element of a commutative ring
be an element of a commutative ring 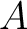 .
Then there is a canonically defined homeomorphism
between
.
Then there is a canonically defined homeomorphism
between 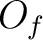 and
and
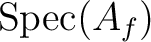 .
(It is usual to identify these two via this homeomorphism.)
.
(It is usual to identify these two via this homeomorphism.)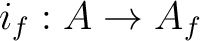 be the natural homomorphism.
We have already seen that we have a continuous map
be the natural homomorphism.
We have already seen that we have a continuous map
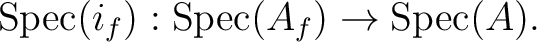
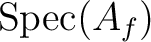 and
and  .
.
Let us do this by considering representations.
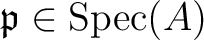 corresponds to a representation
corresponds to a representation
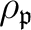 .
.
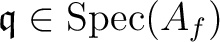 corresponds to a representation
corresponds to a representation
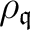 .
.
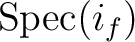 corresponds to a restriction map
corresponds to a restriction map
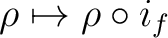 .
.
Now, for any
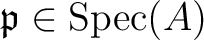 ,
,
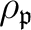 extends to
extends to 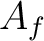 if and only if the image
if and only if the image
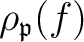 of
of
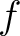 is invertible, that means,
is invertible, that means,
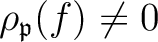 .
In such a case, the extension is unique.
(We recall the fact that the inverse of an element of
a field is unique.)
.
In such a case, the extension is unique.
(We recall the fact that the inverse of an element of
a field is unique.)
It is easy to prove that
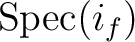 is a homeomorphism.
is a homeomorphism.
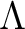
Let 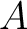 be a ring. Let
be a ring. Let 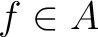 .
It is important to note that each element of
.
It is important to note that each element of 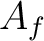 is written as a
“fraction”
is written as a
“fraction”
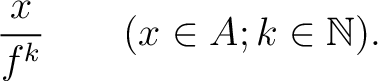
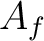 as a set of such formal fractions
which satisfy ordinary computation rules.
In precise, we have the following Lemma.
as a set of such formal fractions
which satisfy ordinary computation rules.
In precise, we have the following Lemma.
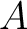 be a ring,
be a ring, 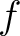 be its element.
We consider the following set
be its element.
We consider the following set
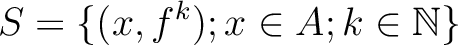
 the following equivalence law.
the following equivalence law.
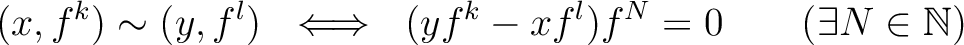
 by introducing
the following sum and product.
by introducing
the following sum and product.
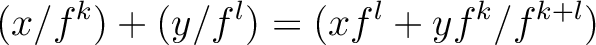
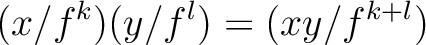
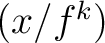 the equivalence class of
the equivalence class of
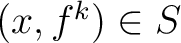 .
.
Likewise, for any 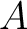 -module
-module 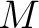 , we may define
, we may define 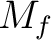 as
a set of formal fractions
as
a set of formal fractions