

Next: 初等的なアプローチ
Up: ガウスの正17角形
Previous: ガウスの正17角形
二乗して 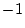 になる数として, 虚数単位
になる数として, 虚数単位 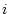 をご存知の方も
多いでしょうが, 4乗して
をご存知の方も
多いでしょうが, 4乗して 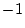 になる数については,
初級段階で触れられることが少ないので,
ここでちょっとだけ述べてみることにします.
になる数については,
初級段階で触れられることが少ないので,
ここでちょっとだけ述べてみることにします.
を解けばよいのです. これを
と因数分解してみると, 後は二次方程式を解くことに帰着されて,
という具合になります. つまり, 4乗して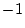 になる数は存在します. (4つもあります)
これらは, 4乗して
になる数は存在します. (4つもあります)
これらは, 4乗して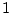 になる数と併せて正8角形の頂点をつくります.
になる数と併せて正8角形の頂点をつくります.
一般に 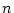 乗して
乗して 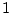 になる数は
になる数は 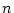 個あり,
それらを順に結ぶと単位円に内接する正
個あり,
それらを順に結ぶと単位円に内接する正 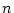 角形ができます.
角形ができます.
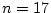 の場合には,
の場合には,
の根全体が, 正 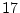 角形を作るわけです.
この方程式の根のうち,
角形を作るわけです.
この方程式の根のうち, 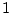 は自明ですから, それを省きましょう.
は自明ですから, それを省きましょう.
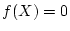 の根は
の根は
です. ただし, ここで
です. ガウスは三角関数をよく知っていたはずですし,
「喋れるようになる前から計算していた」と自ら語るだけの計算達者ですから,
これらの値を手早く計算できたに違いないのですが,
それで終らせはしませんでした.
かれは 19歳のとき, 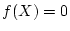 を代数的に解くことができることを発見したのです.
それは上記の数値を求めたり, 正17角形の作図法をあたえる, ということが
面白かったということもまあ多少はあったのでしょうが,
我々があとからいろいろなことを知った後でみてみると,
彼はむしろ方程式(とその根)の構造そのものの美しさをみて喜んだとみるほうが
妥当だと思われます.
を代数的に解くことができることを発見したのです.
それは上記の数値を求めたり, 正17角形の作図法をあたえる, ということが
面白かったということもまあ多少はあったのでしょうが,
我々があとからいろいろなことを知った後でみてみると,
彼はむしろ方程式(とその根)の構造そのものの美しさをみて喜んだとみるほうが
妥当だと思われます.
上の16次方程式 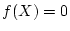 の根は整数から始まって, 足し算, 引き算, かけ算, 平方根
を用いて書くことができます. この仕組みを理解し, 美しさを味わうのが
本文の目標です.
の根は整数から始まって, 足し算, 引き算, かけ算, 平方根
を用いて書くことができます. この仕組みを理解し, 美しさを味わうのが
本文の目標です.
2002-08-15
![]() 乗して
乗して ![]() になる数は
になる数は ![]() 個あり,
それらを順に結ぶと単位円に内接する正
個あり,
それらを順に結ぶと単位円に内接する正 ![]() 角形ができます.
角形ができます.
![]() の場合には,
の場合には,
![]() の根は整数から始まって, 足し算, 引き算, かけ算, 平方根
を用いて書くことができます. この仕組みを理解し, 美しさを味わうのが
本文の目標です.
の根は整数から始まって, 足し算, 引き算, かけ算, 平方根
を用いて書くことができます. この仕組みを理解し, 美しさを味わうのが
本文の目標です.