

Next: 乗法
Up: 平均をとる考え方
Previous: 四分割
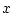 が方程式
が方程式 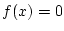 をみたすとき,
をみたすとき, 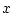 の有理数係数の多項式
の有理数係数の多項式 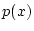 は
は
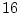 個の根
個の根
の有理数係数の和として書くことができます.
それには次のような手順を踏めばよろしい.
- 1.
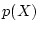 を
を 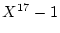 で割った余りを
で割った余りを 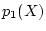 とおく.
これには
とおく.
これには 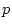 に現れる
に現れる 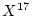 を随時
を随時 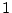 で置き換えればよい.
で置き換えればよい.
- 2.
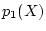 の定数項
の定数項 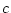 に着目し,
に着目し,
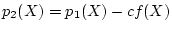 とおく.
とおく.
このとき,
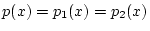 であり,
であり, 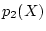 は
は
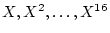 の有理数係数の和ですから,
の有理数係数の和ですから, 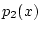 は所定の目的を果たしています.
は所定の目的を果たしています.
たとえば, 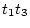 をこの方法で簡易化してみましょう.
をこの方法で簡易化してみましょう.
ステップ 1.で,
定数項が 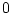 なので, ステップ2は必要なかったですね.
このように簡易化しておくと,
なので, ステップ2は必要なかったですね.
このように簡易化しておくと,
という等式が容易にみてとれます. これがこの簡易化の利点です.
ただし, この簡易化では定数項を 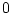 にしているぶん単に定数をあらわすとき
にはかえって面倒になります. たとえば,
にしているぶん単に定数をあらわすとき
にはかえって面倒になります. たとえば,
(本当は 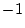 )
のようなちょっとまどろっこしいことが起きていることにも
注意が必要です.
)
のようなちょっとまどろっこしいことが起きていることにも
注意が必要です.
2002-08-15
![]() をこの方法で簡易化してみましょう.
をこの方法で簡易化してみましょう.
![]() にしているぶん単に定数をあらわすとき
にはかえって面倒になります. たとえば,
にしているぶん単に定数をあらわすとき
にはかえって面倒になります. たとえば,