flatness

We define here notion of ``flatness". For non commutative algebras, we need to distinguish ``left-flat" and ``right-flat''. Ironically, Bourbaki's book ``commutative algebra''[1] is one of the best source available on this subject. For the time being, we define flatness for commutative algebras only.

DEFINITION 7.1   Let $A$ be a commutative rings. An $A$ -module $M$ is flat if for any exact sequence

$$0\to N_1\to N_2\to N_3\to 0,$$

a sequence

$$0\to M\otimes_A N_1\to M\otimes_A N_2\to M\otimes_A N_3\to 0$$

is also exact.

Note that we have the following

LEMMA 7.2   Let $A$ be a commutative rings. Let $M$ be an $A$ -module. Then for any exact sequence

$$0\to N_1\overset{f_1}{\to} N_2\overset{f_2}{\to} N_3\to 0$$

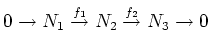
of $A$ -modules, a sequence

$$M\otimes_A N_1\overset{\operatorname{id}_M\otimes f_1}{\to} M\otimes_A N_2\overset{\operatorname{id}_M\otimes f_2}{\to} M\otimes_A N_3\to 0$$

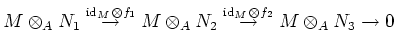
is also exact. Thus $M$ is flat over $A$ if and only if for any module $N_2$ and for any submodule $N_1$ of $N_2$ , the map

$$M\otimes_A N_1 \overset{\operatorname{id}_M\otimes \operatorname{inclusion}}{\longrightarrow} M\otimes_A N_2$$

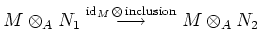
is injective.

PROOF.. Given any element $\sum_i m_i \otimes n_i$ of $M\otimes N_3$ , we take a lift $\hat {n_i}$ of $n_i$ to $N_2$ . Then we have

$$(\operatorname{id}_M\otimes f_2) (\sum_i m_i \otimes \hat{n_i})=\sum_i m_i \otimes n_i.$$

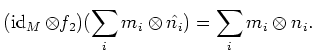
Thus the map $\operatorname{id}_M\otimes f_2$ is surjective. To see the exactness in the middle, we first notice that

$$(\operatorname{id}_M\otimes f_2) \circ (\operatorname{id}_M\otimes f_2)=\operatorname{id}_M \otimes(f_2\circ f_1)=0.$$

Thus $\operatorname{id}\otimes f_2$ yields an $A$ -module homomorphism

$$\phi: (M\otimes_A N_2) /(M\otimes_A N_1)\to M\otimes_A N_3.$$

On the other hand, for any element $(m,n)\in M\times N_3$ , we take a lift $\hat {n}$ of $n$ to $N_2$ and define

$$\alpha: M\times N_3 \ni (m,n) \mapsto [m\otimes\hat n] \in (M\otimes_A N_2) /(M\otimes_A N_1).$$

We may easily check that $\alpha$ is well-defined (independent of the choice of the lift $\hat n$ of $n$ ) and is $A$ -bilinear. So $\alpha$ defines an $A$ -module homomorphism

$$\psi: M\otimes N_3 \ni (m\otimes n) \mapsto [m\otimes \hat n] \in (M\otimes_A N_2) /(M\otimes_A N_1).$$

Then it is easy to show that the homomorphisms $\phi$ and $\psi$ are inverse to each other.

(See for example [14, Appendix A] or [1].)

$\qedsymbol$

DEFINITION 7.3   An $A$ -algebra $B$ is flat if it is flat as an $A$ -module.

A morphism of affine schemes is flat if the corresponding ring homomorphism is flat.

EXAMPLE 7.4   $\mathbb{Z}/3\mathbb{Z}$ is not flat over $\mathbb{Z}$ . Indeed, we consider an exact sequence

$$0\to \mathbb{Z}\overset{\times 3}{\to} \mathbb{Z}\to \mathbb{Z}/3\mathbb{Z}\to 0.$$

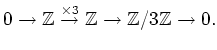
Then by tensoring with $\mathbb{Z}/3\mathbb{Z}$ we obtain a sequence

$$0\to \mathbb{Z}/3\mathbb{Z}\overset{\times 3}{\to} \mathbb{Z}/3\mathbb{Z}\to \mathbb{Z}/3\mathbb{Z}\to 0$$

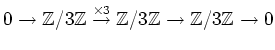
which is not exact.

Let us view it as a homomorphism 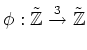$\phi: \tilde{\mathbb{Z}} \overset{3}{\to} \tilde{\mathbb{Z}}$ of quasi coherent sheaf on $\operatorname{Spec}(\mathbb{Z})$ with the keyword ``section wise'' and ``fiber wise'' in mind.

1. $\phi$ is injective if and only if it is injective section wise. Thus our $\phi$ is injective.
2. $\phi$ is ``not injective'' at the fiber of the point $3$ .

EXAMPLE 7.5   Let $k$ be a field. Then a ring homomorphism $k[X]\to k[X,Y]/(XY,Y^2)$ is not flat. The reason is almost the same with the one above. (We consider an exact sequence

$$0\to k[X] \overset{\cdot X}{\to} k[X] \to k[X]/X k[X] \to 0.$$

In this example, an embedded prime $(X,Y)$ of $I=(XY,Y^2)$ in $k[X,Y]$ falls into the zero locus of $X$ .)