

Next: あと書き
Up: 自然対数の底 e
Previous: 三角関数とその一次結合の満たす微分方程式
よく見てみると、前節までに、次のような微分方程式が二種類出てきました。
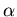 が実数なら、
が実数なら、
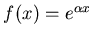 が唯一の解であり、
が唯一の解であり、
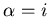 ならば、
ならば、
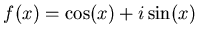 が唯一の解でした。
が唯一の解でした。
でも、こんな場合分けは余り嬉しくない。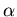 がどんな数であっても、
方程式の解は同様な式で表せた方が便利だ。もし、
がどんな数であっても、
方程式の解は同様な式で表せた方が便利だ。もし、
と決めることができたら、便利だとは思いませんか?
でも、本編でも見たように、便利そうに見えるからといって、
直ちにそう決めてしまうと、失敗することがありますから、
他のいろいろな状況も併せて考える必要があります。
結果からいうと、こう決めるのは実に有効で、現代数学に欠くべからざる公式
の一つになっているのです。
Yoshifumi Tsuchimoto
2000-04-12
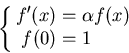
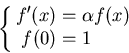
![]() がどんな数であっても、
方程式の解は同様な式で表せた方が便利だ。もし、
がどんな数であっても、
方程式の解は同様な式で表せた方が便利だ。もし、