

Next: 指数関数と三角関数との関係
Up: 自然対数の底 e
Previous: 微分方程式
前節に述べたように、
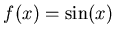 は
は
を満たします。しかし、これは微分を二回も行っているので、
先程の指数関数の微分方程式に比べて、やや複雑です。
このような状況を解決するのに、便利な方法があります。
とやってから、やおら
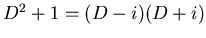 と因数分解し、
と因数分解し、
とやるのです。
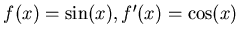 でしたから、
でしたから、
ということになります。
まとめますと、
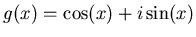 という関数を考えると、
という関数を考えると、
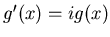 を満たす。
ということになります。ちょっと注意してやれば、
を満たす。
ということになります。ちょっと注意してやれば、
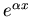 の時と同様の議論をつかうことにより、
の時と同様の議論をつかうことにより、
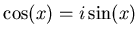 は
は
を満たす唯一の関数だということも示すことができます。
(この節の内容のうち、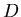 を使う部分は、
「本当にこんなことやって良いの?」という声が上がりそうですが、
大丈夫。注意さえすれば十分正しい議論として通用します。このようなやりかたは、
《演算子法》あるいは《作用素の代数の理論》として知られているものです。)
を使う部分は、
「本当にこんなことやって良いの?」という声が上がりそうですが、
大丈夫。注意さえすれば十分正しい議論として通用します。このようなやりかたは、
《演算子法》あるいは《作用素の代数の理論》として知られているものです。)
Yoshifumi Tsuchimoto
2000-04-12
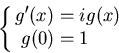
![]() を使う部分は、
「本当にこんなことやって良いの?」という声が上がりそうですが、
大丈夫。注意さえすれば十分正しい議論として通用します。このようなやりかたは、
《演算子法》あるいは《作用素の代数の理論》として知られているものです。)
を使う部分は、
「本当にこんなことやって良いの?」という声が上がりそうですが、
大丈夫。注意さえすれば十分正しい議論として通用します。このようなやりかたは、
《演算子法》あるいは《作用素の代数の理論》として知られているものです。)