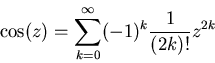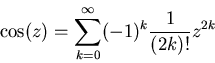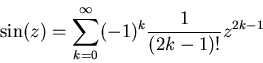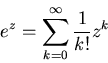

Next: 応用
Up: 指数関数と三角関数
Previous: 三角関数の巾級数表示
巾級数による展開は関数を識別するための「名前」としても
優れている。
実際、個々の関数に
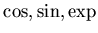 等々の名前をつけても、
その関数の性質はちっとも明らかにならないのにたいし、
関数を巾級数で与えてみると、その巾級数の個々の係数は
関数のもつ性質をかなり雄弁に語ってくれることが多い。
等々の名前をつけても、
その関数の性質はちっとも明らかにならないのにたいし、
関数を巾級数で与えてみると、その巾級数の個々の係数は
関数のもつ性質をかなり雄弁に語ってくれることが多い。
その典型的なものが、この小節で述べる指数関数と対数関数の関係である。
この関係式は、もちろんいろんな形で説明できるが、
巾級数による記述は簡潔で、分かりやすい。
と、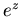 の巾級数展開
の巾級数展開
とから、次のことを見てとることができる。
あるいは、書き換えると、
とくに、上の式で 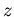 が実数の時だけを考えて、
が実数の時だけを考えて、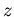 の変わりに
の変わりに 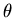 と書くと、
と書くと、
という関係式を得る。
この一見奇妙な関係式は、実にいろいろな応用を持った、
現代数学に決して欠かせない式である。
この式の一つの応用として、
複素数の指数関数を、(高校生卒業程度の知識を持つ諸君にとっては)
見慣れた実関数のみを用いて書き直すことができる。
Yoshifumi Tsuchimoto
2000-04-12