



Next: multidegree monoids and lattices
Up: injectivity ()
Previous: comments on this section
Contents
Lemma 16
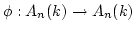
be a

-homomorphism.
Then
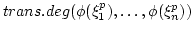
is equal to
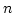
.
[proof]
We may assume that  is algebraically closed. The field
is algebraically closed. The field
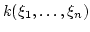 has
has 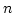 linearly independent
linearly independent  -derivations
-derivations
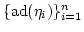 .
Since
.
Since
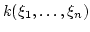 is separable over
is separable over  ,
its transcendent degree is equal to the number of
linear independent derivations [3, Theorem 4.4.2.].
Thus we conclude that transcendent
degree of
,
its transcendent degree is equal to the number of
linear independent derivations [3, Theorem 4.4.2.].
Thus we conclude that transcendent
degree of
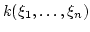 is no less than (hence is equal to)
is no less than (hence is equal to) 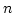 .
That means,
.
That means,
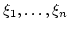 are algebraically independent over
are algebraically independent over  .
.
Lemma 17 (
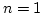
)
Any

-algebra endomorphism
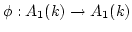
is injective.
[proof]
We may assume that the base field  is algebraically closed.
is algebraically closed.
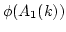 has no zero-divisor except for 0. Thus
is a skew field which is of finite rank over
has no zero-divisor except for 0. Thus
is a skew field which is of finite rank over
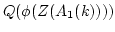 .
If the transcendent degree of the field
.
If the transcendent degree of the field 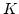 is
is 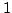 , then it contradicts with
Tsen's theorem.
Thus
, then it contradicts with
Tsen's theorem.
Thus
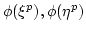 are algebraically independent over
are algebraically independent over  .
.
ARRAY(0x8f0693c)




Next: multidegree monoids and lattices
Up: injectivity ()
Previous: comments on this section
Contents
2003/3/3
![]()