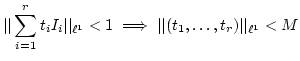Next: injectivity for almost all
Up: Preliminaries on Dixmier conjecture
Previous: injectivity()
Contents
For any element
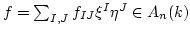 ,
we denote by
,
we denote by
 the multidegree of
the multidegree of 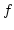 . That means,
. That means,
where we employ the lexicographic order on
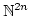 .
For any subalgebra
.
For any subalgebra 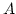 of
of  , we define its multidegree monoid
, we define its multidegree monoid
 as follows.
It is a sub monoid of
as follows.
It is a sub monoid of
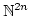 .
We use several norms for indices in
.
We use several norms for indices in
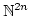 .
Among them is the ``
.
Among them is the ``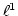 -norm''
-norm''
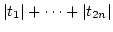 .
of
.
of
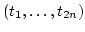 The total degree
The total degree
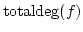 of an element
of an element 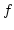 of
of  is then defined to be the
is then defined to be the 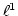 -norm of
-norm of
 .
By a total degree of a derivation or an algebra endomorphism of
.
By a total degree of a derivation or an algebra endomorphism of  we mean the maximum of the total degree of the image of the standard generators
we mean the maximum of the total degree of the image of the standard generators
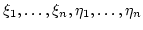 .
.
Definition 2
For any subset
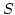
of
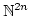
, we denote by
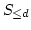
the set
of all elements of
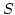
whose
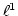
-norms are less than or equal to
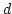
.
We denote by
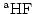
"the affine Hilbert function" of
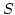
, that is,
For any subalgebra
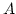
of

, we define its affine Hilbert function
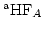
as the affine Hilbert function
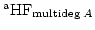
of multidegree of
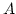
.
Lemma 18
Let
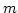
be a positive integer.
Let
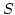
be a sub monoid of
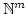
.
Let
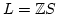
be the submodule of
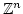
generated by
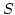
.
Then the following conditions are equivalent.
- There exists a positive real number
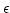 such that
such that
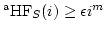 for all
for all 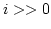 .
.
-
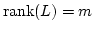
 :
Take
:
Take
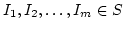 which are linearly independent over
which are linearly independent over
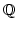 .
Put
.
Put
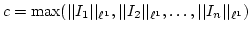 .
Then a map
.
Then a map 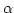 defined by
defined by
is injective and
satisfies
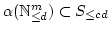 for every positive integer
for every positive integer 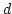 .
Thus we have
when
.
Thus we have
when 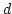 is large enough.
(
is large enough.
(![$ [\bullet]$](img312.png) denotes the Gaussian symbol.)
denotes the Gaussian symbol.)
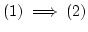 : Assume on the contrary that
: Assume on the contrary that
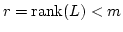 .
Then the module
.
Then the module  , being torsion free, is isomorphic to
, being torsion free, is isomorphic to
 .
Let
.
Let
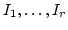 be elements of
be elements of 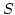 which forms a
which forms a
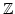 -basis of
-basis of
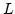 . Then a map
. Then a map
is an injective linear map from
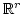 to
to
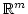 .
Thus we may easily see that there exists a real number
.
Thus we may easily see that there exists a real number 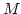 such that
This implies that
such that
This implies that 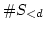 is smaller than the number of elements
of
is smaller than the number of elements
of
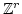 which are shorter (in
which are shorter (in 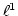 -norm) than
-norm) than 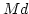 .
.
ARRAY(0x8f2aaf8)
Subsections




Next: injectivity for almost all
Up: Preliminaries on Dixmier conjecture
Previous: injectivity()
Contents
2003/3/3
![]() ,
we denote by
,
we denote by
![]() the multidegree of
the multidegree of ![]() . That means,
. That means,
![]() :
Take
:
Take
![]() which are linearly independent over
which are linearly independent over
![]() .
Put
.
Put
![]() .
Then a map
.
Then a map ![]() defined by
defined by
![$\displaystyle \operatorname{{}^aHF}_S(d)\geq \binom{m+[d/c]}{m} \geq \frac{d^m}{(c+1)^m m!}
$](img311.png)
![]() : Assume on the contrary that
: Assume on the contrary that
![]() .
Then the module
.
Then the module ![]() , being torsion free, is isomorphic to
, being torsion free, is isomorphic to
![]() .
Let
.
Let
![]() be elements of
be elements of ![]() which forms a
which forms a
![]() -basis of
-basis of
![]() . Then a map
. Then a map