



Next: light exponential function
Up: Notations
Previous: Notations
Contents
Lemma 1
Let

be a field of characteristic
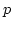
.
Then a

-algebra
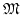
which is generated
by
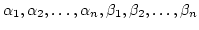
with the relations
(where
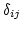
is the Kronecker's delta)
is isomorphic to the full matrix algebra
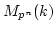
.
Since
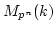 is isomorphic to a tensor product of
is isomorphic to a tensor product of 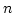 copies of
the matrix algebra
copies of
the matrix algebra 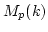 ,
we may assume that
,
we may assume that 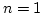 .
We define elements
.
We define elements
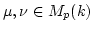 as follows.
as follows.
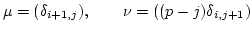 |
(1) |
Then
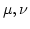 satisfies the same relation as
satisfies the same relation as
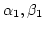 .
In other words, we have a
.
In other words, we have a  -algebra homomorphism
-algebra homomorphism 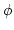 from
from
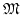 to
to 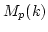 with
with
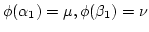 .
.
On the other hand, it is easy to see that the algebra
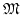 is linearly generated
by
is linearly generated
by
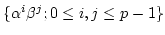 and hence that its dimension
is not greater than
and hence that its dimension
is not greater than 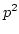 .
.
By a dimension argument we see that the algebra homomorphism
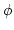 is an isomorphism.
is an isomorphism.
ARRAY(0x8ea145c)




Next: light exponential function
Up: Notations
Previous: Notations
Contents
2003/3/3
![]() satisfies the same relation as
satisfies the same relation as
![]() .
In other words, we have a
.
In other words, we have a ![]() -algebra homomorphism
-algebra homomorphism ![]() from
from
![]() to
to ![]() with
with
![]() .
.
![]() is linearly generated
by
is linearly generated
by
![]() and hence that its dimension
is not greater than
and hence that its dimension
is not greater than ![]() .
.
![]() is an isomorphism.
is an isomorphism.
![]()