可換理論では ![]() は補助的役割しか果たさなかったことを思い出そう。
つまり、
は補助的役割しか果たさなかったことを思い出そう。
つまり、![]() を如何なる値にとろうとも、最終的な答えは (
を如何なる値にとろうとも、最終的な答えは (![]() を
を
![]() で置き換えることにより)同じものになってしまう。
で置き換えることにより)同じものになってしまう。
それに対して、非可換理論においては、![]() は役割を背負った、消去できない
パラメータとして登場している。
これは
は役割を背負った、消去できない
パラメータとして登場している。
これは ![]() の大きさが
の大きさが ![]() と
と
![]() との交換関係
との交換関係
![]() の値が大きい状況とは不確定性が無視できる状況であるということができる。
の値が大きい状況とは不確定性が無視できる状況であるということができる。
![]() を
を ![]() と書き直し、
と書き直し、![]() を
を ![]() とおくと、
とおくと、
![]() は次のような関係式を満たす
は次のような関係式を満たす ![]() で生成された環であると
定義することもできる。
で生成された環であると
定義することもできる。
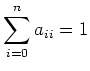 |
||
このかたちで与えた方が、
![]() の《極限》でこの環が可換であるなどという言いかたができて、
好まれるかも知れない。
の《極限》でこの環が可換であるなどという言いかたができて、
好まれるかも知れない。
ともかく、前小節で述べたことにより、
![]() の上の関数環が
行列環で《近似》できたことになる。
の上の関数環が
行列環で《近似》できたことになる。
これは面白い現象だと思われる。この現象については、また立ち戻って調べることに なるだろう。