


: 非可換スキームをつくろう。
: 曲面の非可換変形のいくつかの例について
: 非可換空間の定義
目次
非可換スキームの定義
標語的にいえば、スキームというのは「扱いやすい」アーベル圏の事である
といえる。どの程度扱いやすいのが良いかは場合にもよろうが、
ここでは前節に続いて Rosenberg [7] の見方を採用し、
そのスキームの定義を述べる。
まずは「局所化」の定義である。
Definition 3.1
[
7]
A morphism
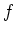
(in the sense of Rosenberg) between categories is said to
be flat if the inverse image functor
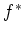
is exact.
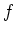
is called a flat
localization if
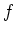
is flat and has a fully faithful direct image functor.
次に、「アファインスキーム」の定義をする。
Definition 3.2
[
7]
A continuous morphism
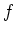
(in the sense of Rosenberg)
between categories is said to
be almost affine if the direct image functor
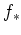
is exact and faithful.
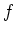
is said to be affine if
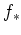
is faithful and has a right adjoint.
この定義がどうして「アファインスキーム」に当たるものを定義していることに
なるのかについては少々注釈が必要だろう。
Monad の定義について思い出しておくことにする。
Definition 3.3
A monad
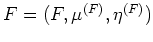
on a category
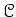
is a functor
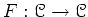
with a natural transformations
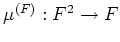
(``multiplication'') and
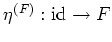
(``unity'')
which satisfies certain axioms
(``associativity'' and ````unity'' being unity'')[
4].
We denote by
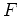
the category of
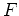
-modules (
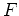
-algebra in the
language of Mac Lane[
4]). By definition, an
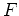
-module is
a pair
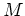
of an object
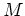
of the category
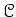
and an arrow
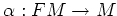
(``action'') which satisfies ``axioms of action''.
詳しくは [4] を参照のこと。
Monad の言葉を使うと上記アファインスキームの定義は次のように言い替えられる
Lemma 3.1
[
7]
Let
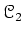
be an abelian category. For any right-exact monad
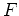
on
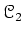
, we have a morphism
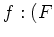
-
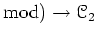
.
A continuous morphism
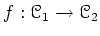
is almost affine if and only if
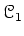
is equivalent over
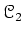
to
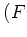
-

for some right-exact monad
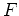
on
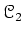
.
Monad の代表例として次のものがある。
Example
Let
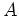
be an algebra and
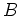
an
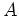
-algebra. Then a functor
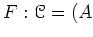
-
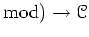
given by tensor products
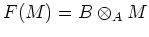
is a monad.
The category
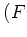
-

is isomorphic to the category
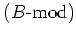
of
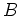
-modules. The morphism
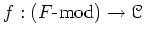
in this case
is identified with the morphism associated to the structure morphism
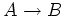
.
以上のことから、
環準同型 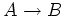 があれば
があれば
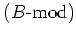 は
は
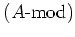 上の
アファインスキームとみなすことができることが分かる。
上の
アファインスキームとみなすことができることが分かる。
一般の monad を扱う時には、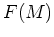 を心の中で
を心の中で
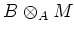 と読みかえて
ダイアグラムを書くと、上の例と同様に処理できることが多い。例えば、
次の補題のような調子である。
と読みかえて
ダイアグラムを書くと、上の例と同様に処理できることが多い。例えば、
次の補題のような調子である。
Lemma 3.2
Let
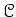
be an abelian category. Let
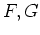
be monads on
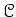
.
Let
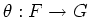
be a morphism of monads [
4].
Then there exists a morphism (in the sense of Rosenberg) such that
its direct- and inverse image functors are given as follows.
where the symbol
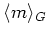
denotes a ``
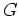
-submodule of
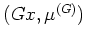
generated by a sub object
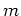
of
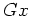
''. That is,
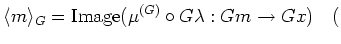
$&lambda#lambda;:m &rarr#to;Gx$ is the inclusion)
お待ちかねのスキームの定義は次のようになる。
Definition 3.4
[
7]
A set of flat localizations
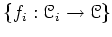
is said to be a
Zariski cover of
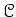
if any arrow
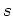
of
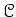
such that
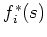
is
invertible for all
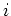
is invertible.
A continuous morphism
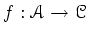
is said to be a quasi-scheme over
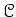
if there exists a Zariski cover
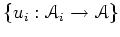
such that
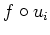
is almost affine for each
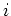
.
上のスキームの定義は、「局所的にアファイン」と言う従来の
スキームの定義をカテゴリーの言葉を使って非可換の場合にまで
拡張した物で、分かりやすいが、この定義がどのくらい良いかは、あとあとの
判断を待たねばなるまい。
非可換空間の例としてアファインスキームの次に現れるのは、
やはり射影「スキーム」であろう。
Definition 3.5 (See [
2] and references cited there.)
Let
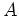
be an
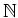
-graded algebra
We define the projective spectrum of
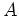
as follows.
where ``(Torsion)'' is a collection of modules
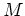
which satisfy the
following property.
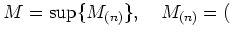
elements of $M$ annihilatate by $R_>n$
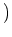
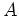 の乗法が適当な交換関係(Ore property) を持てば、
の乗法が適当な交換関係(Ore property) を持てば、
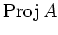 は
Rosenberg の意味のスキームになる。一般にはおそらく
は
Rosenberg の意味のスキームになる。一般にはおそらく
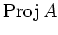 は Rosenberg の意味のスキームにならないこともあると思われる。
(が、「スキームにならない」証明は難しそうである。)
要は非可換空間が Rosenberg の意味のスキームになっていれば可換理論と
平行な理論が進む幸運に感謝しながら先を進め、
そうなっていなければ他の意味で「扱いやすい」かどうか検討してみれば良いのである。
は Rosenberg の意味のスキームにならないこともあると思われる。
(が、「スキームにならない」証明は難しそうである。)
要は非可換空間が Rosenberg の意味のスキームになっていれば可換理論と
平行な理論が進む幸運に感謝しながら先を進め、
そうなっていなければ他の意味で「扱いやすい」かどうか検討してみれば良いのである。



: 非可換スキームをつくろう。
: 曲面の非可換変形のいくつかの例について
: 非可換空間の定義
目次
平成15年9月1日
![]() があれば
があれば
![]() は
は
![]() 上の
アファインスキームとみなすことができることが分かる。
上の
アファインスキームとみなすことができることが分かる。
![]() を心の中で
を心の中で
![]() と読みかえて
ダイアグラムを書くと、上の例と同様に処理できることが多い。例えば、
次の補題のような調子である。
と読みかえて
ダイアグラムを書くと、上の例と同様に処理できることが多い。例えば、
次の補題のような調子である。
![]() の乗法が適当な交換関係(Ore property) を持てば、
の乗法が適当な交換関係(Ore property) を持てば、
![]() は
Rosenberg の意味のスキームになる。一般にはおそらく
は
Rosenberg の意味のスキームになる。一般にはおそらく
![]() は Rosenberg の意味のスキームにならないこともあると思われる。
(が、「スキームにならない」証明は難しそうである。)
要は非可換空間が Rosenberg の意味のスキームになっていれば可換理論と
平行な理論が進む幸運に感謝しながら先を進め、
そうなっていなければ他の意味で「扱いやすい」かどうか検討してみれば良いのである。
は Rosenberg の意味のスキームにならないこともあると思われる。
(が、「スキームにならない」証明は難しそうである。)
要は非可換空間が Rosenberg の意味のスキームになっていれば可換理論と
平行な理論が進む幸運に感謝しながら先を進め、
そうなっていなければ他の意味で「扱いやすい」かどうか検討してみれば良いのである。