![]() 上の半単純 Lie 環
上の半単純 Lie 環 ![]() を考えよう。
普遍包絡環
を考えよう。
普遍包絡環
![]() が定義される。この環に対して
我々の議論を適用したい。
が定義される。この環に対して
我々の議論を適用したい。
まず ![]() はカルタン行列による表示をもつ。
はカルタン行列による表示をもつ。
そこで、![]() の生成元としてこの
の生成元としてこの
![]() を採用し、
を採用し、
以下の所論には ![]() のもう少し詳しい情報が必要である。
のもう少し詳しい情報が必要である。
これらのデータを標数 ![]() の世界に落とそう。
の世界に落とそう。![]() からはじめたわけだから落とした体としては
からはじめたわけだから落とした体としては
![]() で十分であるわけだが、フロベニウス写像の作用を詳細に見るために
ここでは標数
で十分であるわけだが、フロベニウス写像の作用を詳細に見るために
ここでは標数 ![]() の体
の体 ![]() を考えて、
を考えて、![]() について考察する。
について考察する。
標数 ![]() の世界では、restricted Lie 環の概念が存在する[3]。
正標数の半単純 Lie 環は restricted Lie 環の代表例である。
Lie 環の一般論をここで繰り広げるわけにはいかぬだろうから、
無理矢理に次のようにまとめておこう。
の世界では、restricted Lie 環の概念が存在する[3]。
正標数の半単純 Lie 環は restricted Lie 環の代表例である。
Lie 環の一般論をここで繰り広げるわけにはいかぬだろうから、
無理矢理に次のようにまとめておこう。
今の場合、 ![]() が
が ![]() の構造定数(や分母に現れる数)
よりも十分大きいという仮定のもとで、
の構造定数(や分母に現れる数)
よりも十分大きいという仮定のもとで、
| (*) |
注意
普遍包絡環にはもっとたくさん中心元がある。casimir 作用素はその
代表的なものであるし、一般的に、標数 0 の半単純リー環 ![]() の
ランク(Cartan sub algebra の次数)を
の
ランク(Cartan sub algebra の次数)を ![]() とすると、
とすると、
![]() の普遍包絡環の中心
の普遍包絡環の中心
![]() は
は ![]() 変数の多項式環である。
(記号
変数の多項式環である。
(記号
![]() は[2] の 23.3 の証明のところのものと
同一である。そこの所論と、Coxeter 群の一般論を用いれば
は[2] の 23.3 の証明のところのものと
同一である。そこの所論と、Coxeter 群の一般論を用いれば
![]() が
多項式環であることがわかる。)
したがって、
が
多項式環であることがわかる。)
したがって、
![]() の元を modulo
の元を modulo ![]() に落としたものが
に落としたものが ![]() のほうにも出てくることになる。
のほうにも出てくることになる。
Poincare-Birkoff-Witt の定理により、(*)の元は ![]() 上独立である。
したがって、(*)で生成される可換環
上独立である。
したがって、(*)で生成される可換環
![]() は生成元の取り方に依存していそうに見えるが実はそうではない。
このことを見るために、
は生成元の取り方に依存していそうに見えるが実はそうではない。
このことを見るために、
![]() から
から
![]() への
写像
への
写像 ![]() を
を
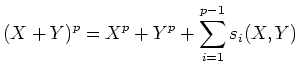 | ||
![$\displaystyle (X+Y)^{[p]}=X^{[p]}+Y^{[p]}+\sum_{i=1}^{p-1} s_i(X,Y)$](img304.png) |
![]() は
は ![]() の像で生成される
可換環である。上記 Poincare-Birkoff-Witt の定理による議論は、
の像で生成される
可換環である。上記 Poincare-Birkoff-Witt の定理による議論は、![]() が単射であることを示している。
とくに、
が単射であることを示している。
とくに、
![]() は
は ![]() のベクトル空間としての双対空間
のベクトル空間としての双対空間 ![]() (を Frobenius 写像によってひねったもの)と標準的に同型である。
(を Frobenius 写像によってひねったもの)と標準的に同型である。
![]() はその上の
はその上の
![]() -coherent な
algebra sheaf であって、
-coherent な
algebra sheaf であって、
![]() -加群としては locally free である。
標準ファイバーは [3] で「
-加群としては locally free である。
標準ファイバーは [3] で「 ![]() の u-algebra」と呼ばれているもの
になる。
の u-algebra」と呼ばれているもの
になる。
こうして、
![]() には
には ![]() が対応するという、
表面上は至極当然な結論にたどり着く。
ただし、上述のalgebra sheaf の存在など、
面白い構造が更につけ加わっているとことが興味深い。
が対応するという、
表面上は至極当然な結論にたどり着く。
ただし、上述のalgebra sheaf の存在など、
面白い構造が更につけ加わっているとことが興味深い。
後記: この小節の内容はオリジナルではあるが、実は math.RT/0401002 などに同様の記述があることがあとでわかった。 (京大の望月拓郎先生の御指摘による。)
| 780-8520 高知市曙町 2-5-1 | ||
| 高知大学理学部 数理情報科学科数理科学コース
| ||
| e-mail: docky@math.kochi-u.ac.jp |
ARRAY(0x90db74c)