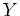 の点(すなわち、
の点(すなわち、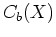 の極大イデアル)
の極大イデアル)
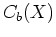 から
から  への
への 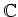 -代数としての準同型
-代数としての準同型 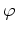
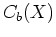 から
から 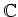 への
への 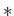 -環準同型
-環準同型
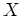 の最大コンパクト化(Stone-Cechコンパクト化)の点
の最大コンパクト化(Stone-Cechコンパクト化)の点
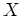 の ultra filter
の ultra filter
こう言い換えてみると ultra filter は ![]() の最大コンパクト化の元で、
principal ultra filter はそのうち
の最大コンパクト化の元で、
principal ultra filter はそのうち ![]() のもともとの元。 non-principal
ultra filter のほうは
のもともとの元。 non-principal
ultra filter のほうは ![]() の``理想境界'' の元であると見ることができて、
若干見やすく感じられると思うのだが、いかがだろう。
の``理想境界'' の元であると見ることができて、
若干見やすく感じられると思うのだが、いかがだろう。
上の補題の証明は本題とは全く関係ないのだが、適当な参考文献が
見当たらないので一応つけておこう。
(この補題が知られていないと言う意味ではない。それどころかいまでは wikipedia
(誰でも書き込めるweb 上の百科事典。 URL は
http://en.wikipedia.org/wiki/ )
にも本質的な部分は載っているぐらいに有名である。)
とくに興味がある方を除いては
次の小節までスキップすることをお勧めする。
![]() は可換
は可換 ![]() -代数(とくにBanach 環)であり、その極大イデアル
-代数(とくにBanach 環)であり、その極大イデアル
![]() は 必ず閉じている(
は 必ず閉じている(
![]() の閉包も
の閉包も ![]() の
イデアルであるから。)。とくに、
の
イデアルであるから。)。とくに、
![]() は Banach 環で、
かつ、体である。そのようなものは
は Banach 環で、
かつ、体である。そのようなものは ![]() しかない。(Gelfand-Mazur の定理。
代数幾何における 零点定理の
しかない。(Gelfand-Mazur の定理。
代数幾何における 零点定理の ![]() -代数版と言っても
(言っている人は見たことがないが、)よかろう。)
ゆえに、(3)のデータが得られる。このことから (1)-(3)の同等性は
明白だろう。
-代数版と言っても
(言っている人は見たことがないが、)よかろう。)
ゆえに、(3)のデータが得られる。このことから (1)-(3)の同等性は
明白だろう。
(4) と(1) の同等性を示そう。
![]() からコンパクトハウスドルフ集合
からコンパクトハウスドルフ集合 ![]() への連続写像
への連続写像 ![]() が
与えられているとする。
が
与えられているとする。
![]() 上の複素数値連続関数全体のなす環
上の複素数値連続関数全体のなす環 ![]() から任意に
から任意に ![]() をとると、
をとると、
![]() は(コンパクト集合上の連続関数であるから)有界で、その
は(コンパクト集合上の連続関数であるから)有界で、その ![]() による
引き戻し
による
引き戻し ![]() も
当然有界である。したがって、
も
当然有界である。したがって、
(5) のデータ、すなわち ![]() の ultra filter
の ultra filter
![]() から
(3)のデータを作ろう。
から
(3)のデータを作ろう。
![]() の元
の元 ![]() を任意にとる。
を任意にとる。![]() に対してその 「
に対してその 「
![]() での
値」(極限) を定める必要があるわけだが、それには「区間縮小法」を用いる。
での
値」(極限) を定める必要があるわけだが、それには「区間縮小法」を用いる。
![]() は有界であるから、ある
は有界であるから、ある ![]() があって、
があって、
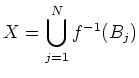 disjoint union
disjoint union